Sumário
Diagonal Secundária - Atenção: Com o algorítimo utilizado podemos efetuar a soma de qualquer matriz quadrada não sendo somente uma matriz 3x3.
Antes de começarmos temos que fala sobre a diferença na indexação.
A diferença na indexação entre a matemática (onde muitas vezes começamos a contar a partir de 1) e a programação (onde começamos a contar a partir de 0) é uma fonte comum de confusão para iniciantes na programação. Vamos explorar essa diferença e explicar como ela afeta o acesso aos elementos em uma matriz.
Matemática: Indexação começando por 1
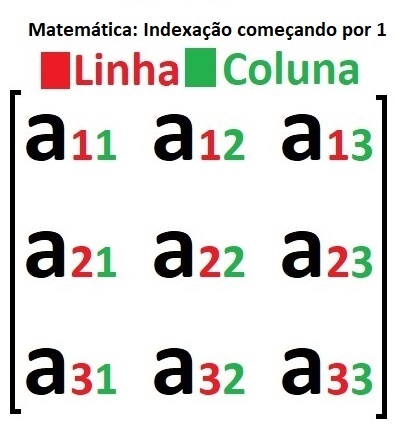
Na matemática e em muitas áreas de estudo acadêmico, como em álgebra linear e teoria dos grafos, é comum começar a contar a partir do número 1. Por exemplo, ao descrever uma matriz ou um sistema de coordenadas:
- Matriz: Os elementos são identificados com dois índices, onde o primeiro índice representa a linha e o segundo índice representa a coluna.
Em uma matriz 3x3, por exemplo, o elemento na primeira linha e primeira coluna é referido como (1,1), na segunda linha e segunda coluna é (2,2), e assim por diante.
Programação: Indexação começando por 0
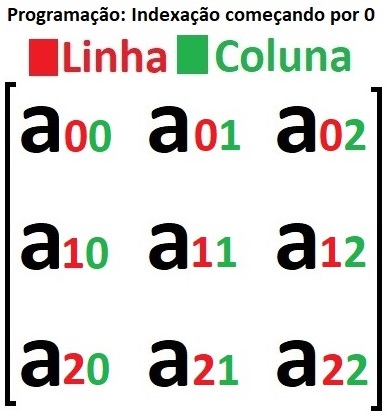
Por outro lado, na programação e na maioria das linguagens de programação, a indexação geralmente começa em 0. Isso significa que o primeiro elemento em uma lista, array ou matriz é acessado pelo índice 0, o segundo pelo índice 1, e assim por diante. Isso é especialmente comum em linguagens como Python, C, Java, JavaScript, entre outras.
Depois desse esclarecimento, vamos continuar!!
Introdução
Vou contar uma história incrível sobre programação Python e matrizes. Vamos aprender a somar a diagonal secundária de uma matriz 3×3 em Python. É um mistério que mistura matemática e programação.
As matrizes em Python são muito fortes e usadas em muitos lugares. Saber lidar com elas é crucial para programadores. Vamos aprender a fazer isso, focando na diagonal secundária e sua soma.
Em muitos problemas de programação, lidamos com matrizes e suas operações. A soma dos elementos localizados na diagonal secundária de uma matriz é uma operação frequente. Vamos explorar como fazer isso em Python de maneira eficiente e compreensível.

Este artigo é perfeito para quem está começando ou quer melhorar em Python e matrizes. Vou te mostrar tudo, desde criar a matriz até somar a diagonal secundária. Vou usar exemplos e dicas para te ajudar.
Principais Pontos.
• Entendimento básico de matrizes em Python
• Identificação da diagonal secundária em uma matriz 3×3
• Implementação do algoritmo de soma em Python
• Otimização do código para melhor desempenho
• Aplicações práticas da soma da diagonal secundária
• Comparação com outras operações matriciais
• Dicas de boas práticas em programação Python
Introdução às Matrizes em Python.
As matrizes em Python são essenciais para organizar e manipular dados. Elas são fundamentais na programação. Vamos entender seu conceito, como são representadas e sua importância.
O que são matrizes?
Matrizes são conjuntos de elementos em linhas e colunas. Em Python, são feitas com listas aninhadas. Cada lista interna é uma linha da matriz.
Como representar matrizes em Python.
Em Python, matrizes são listas de listas. Cada lista interna é uma linha. Vejamos um exemplo de matriz 3x3:
matriz = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
Essa configuração torna mais fácil acessar e manipular os elementos. Isso é feito usando índices.
Importância das matrizes na programação.
Matrizes são cruciais em várias áreas da programação e ciência de dados. Elas são usadas para:
• Armazenar e processar dados tabulares
• Representar imagens digitais
• Realizar cálculos complexos em álgebra linear
• Implementar algoritmos de aprendizado de máquina
Manipular matrizes em Python é essencial. Isso contribui para a criação de soluções em análise de dados, processamento de imagens e inteligência artificial.
| Tipo de Matriz | Descrição | Exemplo em Python |
|---|---|---|
| Matriz Quadrada | Número de linhas igual ao de colunas | [[1, 2], [3, 4]] |
| Matriz Retangular | TNúmero de linhas diferente do de colunas | [[1, 2, 3], [4, 5, 6]] |
| Matriz Identidade | Diagonal principal com 1, resto 0 | [[1, 0], [0, 1]] |
Entendendo a Diagonal Secundária de uma Matriz.
Na matriz quadrada, como na matriz 3x3, a diagonal secundária é formada pelos elementos que se estendem da esquina superior direita até a esquina inferior esquerda. Por exemplo, na matriz abaixo, os elementos da diagonal secundária estão com a cor laranja.
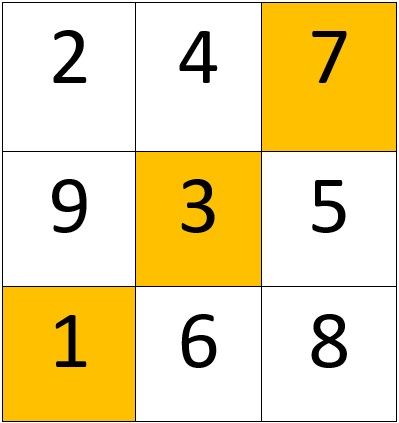
Para somar esses elementos, basta adicionar os valores. Isso é muito usado em estatística e álgebra linear.
A diagonal secundária traz informações únicas da matriz. Ela é muito importante em operações com matrizes. Por exemplo, no cálculo do determinante.
"A diagonal secundária é como um espelho da diagonal principal, revelando características simétricas da matriz."
Entender a diagonal secundária é crucial para quem trabalha com matrizes. Ela ajuda a analisar mais a fundo e a encontrar soluções criativas em vários problemas.
Preparando o Ambiente Python para Manipulação de Matrizes.
Para iniciar a programação em Python e trabalhar com matrizes, é necessário configurar o ambiente. Vamos configurar tudo para que você trabalhe bem com algoritmos em Python.
Instalação do Python e Bibliotecas.
O primeiro passo é instalar o Python no seu computador. Visite o site oficial python.org e baixe a última versão. Na instalação, escolha "Add Python to PATH" para usar mais facilmente.
Depois de instalar, abra o terminal. Digite:
• pip install numpy
• pip install pandas
Essas bibliotecas são essenciais para manipular dados em Python.
Exemplo de um código com a biblioteca Numpy.
Para calcular a soma da diagonal secundária de uma matriz em NumPy, você pode usar a função np.fliplr() para inverter a matriz da esquerda para a direita.
import numpy as np
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
soma_diagonal_secundaria = np.trace(np.fliplr(matriz))
print(f"Soma da diagonal secundária: {soma_diagonal_secundaria}")
Ou, alternativamente, você pode calcular a soma da diagonal secundária usando a indexação:
import numpy as np
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
soma_diagonal_secundaria = np.sum(matriz[np.arange(matriz.shape[0]), matriz.shape[1] - 1 - np.arange(matriz.shape[0])])
print(f"Soma da diagonal secundária: {soma_diagonal_secundaria}")
Ambas as abordagens vão te dar a soma da diagonal secundária da matriz.
Configuração do Ambiente.
Escolha um editor de código que você goste. Visual Studio Code e PyCharm são ótimas escolhas para Python. Eles têm recursos avançados para programar.
Importando Módulos para Operações Matriciais.
Para lidar com matrizes, usaremos o NumPy. No começo do seu script, coloque:
• import numpy as np
Com isso, você está pronto para criar e manipular matrizes em Python! Agora, podemos aprofundar em algoritmos mais avançados e na análise de dados.
Criando uma Matriz 3x3 em Python.
As matrizes são muito importantes na programação Python. Elas ajudam a organizar informações em duas dimensões. Vou mostrar como fazer uma matriz 3x3 de forma fácil.

Para fazer uma matriz, usamos listas aninhadas. Cada lista dentro é uma linha da matriz. Veja um exemplo de matriz 3x3:
matriz = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
Essa forma é simples e perfeita para matrizes pequenas. Para matrizes maiores, usamos compreensão de lista:
matriz = [[0 for j in range(3)] for i in range(3)]
Esse código cria uma matriz 3x3 cheia de zeros. É útil para começar uma matriz vazia e preenchê-la depois.
Ao trabalhar com matrizes em Python, é importante lembrar que elas são representadas como listas de listas. Isso permite acessar e mudar elementos um a um:
matriz[0][1] = 10 # Altera o elemento na primeira linha, segunda coluna
Saber criar e manipular matrizes é essencial em Python. Isso é muito importante em análise de dados e ciência de computação.
Calculando a Soma dos Elementos da Diagonal Secundária de uma Matriz 3×3 Python.
Vamos ver como somar a diagonal secundária de uma matriz 3×3 em Python. Esse processo é essencial em algoritmos e operações com matrizes. Primeiro, vamos saber quais elementos usar. Depois, vamos criar o algoritmo. Por fim, vamos otimizar o código.
Identificando os Elementos da Diagonal Secundária.
O algoritmo para somar esses elementos é simples:
1. Crie uma variável para armazenar a soma.
2. Percorra a matriz, somando os elementos da diagonal secundária
3. Retorne o resultado final
Aqui está um exemplo de código usando uma função:
def soma_diagonal_secundaria(matriz):
soma = 0
for i in range(3):
soma += matriz[i][2-i]
return soma
Otimizando o Código para Eficiência.
Para tornar o código mais rápido, usamos list comprehension. Essa feature do Python é muito útil:
“Em Python, uma função lambda é uma maneira de criar funções pequenas e anônimas de forma concisa.”
soma_diagonal_secundaria = lambda matriz: sum(matriz[i][2-i] for i in range(3))
Essa versão é mais rápida e fácil de entender. Lembre-se, ao programar em Python, é importante ser claro e rápido.
Implementação Passo a Passo do Algoritmo.
Vamos aprender a programar em Python para somar a diagonal secundária. Esse algoritmo é excelente para aprimorar suas habilidades de programação.

Primeiro, criamos uma matriz 3x3 com listas aninhadas. Depois, começamos a somar tudo. Nós focamos nos elementos da diagonal secundária.
Aqui está o código passo a passo:
1. Definir a matriz 3x3
2. Inicializar a variável de soma
3. Iterar sobre as linhas da matriz
4. Somar os elementos da diagonal secundária
5. Imprimir o resultado
Veja como fica o código completo:
| Passo | Código Python |
|---|---|
| 1 | matriz = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] |
| 2 | soma = 0 |
| 3-4 | for i in range(3): soma += matriz[i][2-i] |
| 5 | print(f"A soma da diagonal secundária é: {soma}") |
Este algoritmo em Python mostra como a programação resolve problemas matemáticos. Praticar essas técnicas melhora suas habilidades em Python e análise de dados.
Testando o Código com Diferentes Matrizes.
Desenvolvemos um algoritmo para somar a diagonal secundária. É essencial testá-lo com várias matrizes. Isso assegura que nossa solução funcione bem em vários contextos.
Casos de teste simples.
Primeiro, testamos com matrizes 3x3 e números inteiros positivos. Esses testes básicos ajudam a ver se o código faz os cálculos corretamente.
| Matriz | Soma da Diagonal Secundária |
|---|---|
| [[1 2 3] [4 5 6] [7 8 9]] | 15 |
| [[2 4 6] [8 10 12] [14 16 18]] | 30 |
Matrizes com números negativos e decimais.
Depois, testamos com números negativos e decimais. Essa etapa é crucial para ver se o algoritmo funciona com diferentes números.
Verificação de resultados.
Para cada teste, comparamos o resultado do algoritmo com cálculos feitos à mão. Essa verificação cuidadosa garante a precisão do código em várias situações.
Com esses testes, confirmamos que nosso algoritmo é eficaz para somar a diagonal secundária. Ele funciona bem com diferentes tipos de matrizes 3x3.
Exemplo de um código sem o uso de bibliotecas e pode ser utilizado para qualquer matriz quadrada.
def obter_numero(mensagem):
while True:
try:
return int(input(mensagem))
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
def verifica_matriz(num_linhas, num_colunas):
if num_linhas != num_colunas:
print(
'\033[1;31mErro: Esta implementação suporta apenas matrizes quadradas (mesmo número de linhas e colunas). '
'Reiniciando o programa...\033[m')
main() # Reinicia o programa
def criar_matriz(num_linha, num_coluna):
matriz = []
for linha_numero in range(num_linha):
linha = []
for coluna_numero in range(num_coluna):
while True:
try:
valor = int(
input(f'\033[1;35mPor Favor, digite o {coluna_numero + 1}º elemento da {linha_numero + 1}º '
f'linha: \033[m'))
linha.append(valor)
break
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
matriz.append(linha)
return matriz
def soma_diagonal_secundaria(matriz):
n = len(matriz)
assert n == len(matriz[0]), 'A matriz precisa ser quadrada'
diagonal_secundaria = [matriz[i][n - 1 - i] for i in range(n)]
soma_diagonal_secundaria = sum(diagonal_secundaria)
return diagonal_secundaria, soma_diagonal_secundaria
def mostrar_matriz(matriz_gerada):
print()
print(f'\033[1;36mMatriz gerada\033[m')
for mostra_matriz in matriz_gerada:
print(f'\033[1;36m{mostra_matriz}\033[m')
def main():
print('\033[1;41m*** Inicializando o programa ***\033[m\n')
numero_linhas = obter_numero('\033[1;34mDigite o número de linhas da matriz: \033[m')
numero_colunas = obter_numero('\033[1;34mDigite o número de colunas da matriz: \033[m')
print()
verifica_matriz_quadrada(numero_linhas, numero_colunas)
matriz = criar_matriz(numero_linhas, numero_colunas)
mostrar_matriz_gerada(matriz)
diagonal_secundaria, soma_diagonal_secundaria = soma_e_mostra_diagonal_secundaria(matriz)
print(f"\033[1;34mOs elementos da diagonal secundária são: {diagonal_secundaria}.\033[m")
print(f"\033[1;34mA soma dos elementos da diagonal secundária é: {soma_diagonal_secundaria}.\033[m")
if __name__ == "__main__":
while True:
main()
continuar = input('\033[1;35mDeseja calcular para outra matriz? (s/n): \033[m').lower()
if continuar != 's':
print('\033[1;33mFinalizando o programa!!!!\033[m')
break
Explicando o código
Este código Python implementa um programa interativo para criar e operar em matrizes quadradas. Vamos analisar cada função e como elas funcionam juntas para realizar as operações desejadas:
Função `obter_numero(mensagem)`
Esta função solicita ao usuário que digite um número inteiro através da função `input`. Se ocorrer um erro de `ValueError` (ou seja, se o usuário não digitar um número inteiro), a mensagem de erro é exibida em vermelho (com formatação ANSI para cores) e o loop continua até que o usuário forneça um valor válido. O número inteiro válido é então devolvido.
Função `criar_matriz(num_linha, num_coluna)`
Esta função cria uma matriz solicitando que o usuário insira os elementos linha por linha. Se um valor inválido (não inteiro) for inserido, uma mensagem de erro é exibida e o usuário é solicitado novamente para inserir o valor correto. A matriz final é retornada como uma lista de listas.
Função `soma_diagonal_secundaria(matriz)`
Esta função calcula e retorna os elementos da diagonal secundária da matriz, bem como a soma desses elementos. Primeiro, verifica se a matriz é quadrada. Em seguida, itera sobre os elementos da diagonal secundária usando a compreensão de lista e calcula a soma desses elementos.
Utilização de Cores ANSI
O código utiliza códigos ANSI para colorir o texto na saída do console, tornando a interface mais interativa e informativa para o usuário.
Espero que essa explicação ajude a entender como o código funciona e como ele foi estruturado para lidar com matrizes quadradas, cálculo de diagonal secundária e interação com o usuário de forma amigável.
Aplicações Práticas da Soma da Diagonal Secundária.
A soma da diagonal secundária em matrizes é muito útil em áreas como processamento de imagens, análise de dados e engenharia. Vamos conferir alguns exemplos de como ela é utilizada.

Em imagens, essa técnica ajuda a encontrar bordas e padrões diagonais. É fundamental para reconhecimento facial e detecção de objetos. Usar Python com bibliotecas como OpenCV torna isso possível.
Na análise de dados, ela ajuda a encontrar tendências em dados complexos. Por exemplo, em matrizes de correlação, mostra relações entre variáveis. A biblioteca NumPy facilita muito essas tarefas.
Na engenharia, essa operação é usada para cálculos estruturais e análise de tensões. Ela mostra como as forças estão distribuídas, ajudando a fazer edifícios e pontes mais seguros.
| Campo | Aplicação | Ferramenta Python |
|---|---|---|
| Processamento de Imagens | Detecção de bordas | OpenCV |
| Análise de Dados | Correlação de variáveis | NumPy |
| Engenharia | Análise estrutural | SciPy |
Essas aplicações mostram a importância das operações em matrizes e algoritmos em Python. Saber manipular dados matriciais é essencial para resolver problemas complexos em vários campos. É uma habilidade extremamente valiosa para programadores e cientistas de dados.
Comparação com Outras Operações Matriciais.
Explorar operações em matrizes é fascinante. Vamos ver como a soma da diagonal secundária se compara com outras. Isso nos ajuda a entender melhor os cálculos matemáticos.
Soma da diagonal principal vs. secundária.
A diagonal principal e a secundária são semelhantes, mas focam em coisas diferentes. A diagonal principal vai do canto superior esquerdo ao inferior direito. Já a secundária vai do canto oposto. Ambas são importantes para análise de simetria e propriedades matriciais em Python.
Determinante e traço da matriz.
O determinante e o traço são fundamentais na álgebra linear. O determinante mostra se a matriz é invertível. O traço é a soma dos elementos da diagonal principal da matriz. Essas operações são essenciais em física quântica e aprendizado de máquina.
Operações de transposição e inversão.
A transposição muda as linhas por colunas, mudando a matriz. A inversão encontra a matriz que, multiplicada pela original, dá a matriz identidade. Essas operações são fundamentais em sistemas lineares e transformações geométricas.
| Operação | Complexidade | Aplicação Comum |
|---|---|---|
| Soma Diagonal Secundária | O(n) | Análise de Simetria |
| Determinante | O(n³) | Sistemas Lineares |
| Transposição | O(n²) | Transformações Geométricas |
Cada operação tem seu papel nos cálculos matemáticos. A escolha varia conforme o contexto e o problema a ser resolvido.
Dicas de Otimização e Boas Práticas.
Na programação em Python, otimizar algoritmos é fundamental para resolver problemas de maneira eficiente. Uma dica importante é usar compreensões de lista para criar e manipular matrizes. Essa técnica torna o código mais conciso e rápido, comparado a loops tradicionais.
Outra prática recomendada é usar bibliotecas especializadas, como o NumPy, para operações matriciais complexas. O NumPy oferece funções otimizadas que são mais rápidas e eficientes em memória que implementações manuais.
| Técnica | Benefício | Exemplo |
|---|---|---|
| Compreensões de lista | Código conciso e rápido | [sum(row) for row in matriz] |
| Uso do NumPy | Operações otimizadas | np.sum(matriz, axis=1) |
| Evitar loops aninhados | Melhora o desempenho | sum(matriz[i][i] for i in range(len(matriz))) |
Aplicando essas técnicas, você melhora a eficiência dos seus algoritmos em Python. Além disso, desenvolve habilidades valiosas para resolver problemas em programação Python.
Conclusão
Neste artigo, exploramos o fascinante mundo das matrizes em Python. Focamos na tarefa de calcular a soma da diagonal secundária de uma matriz 3×3. Essa habilidade é essencial para quem quer melhorar em programação Python.
As matrizes em Python são ferramentas poderosas. Elas representam dados multidimensionais de forma eficiente. Calcular a soma da diagonal secundária envolve conceitos importantes de indexação e iteração.
Ao dominar essas técnicas, você estará pronto para desafios mais complexos em programação Python. Isso vale para análise de dados, computação científica ou desenvolvimento de jogos. Pratique regularmente e explore outras operações matriciais para melhorar suas habilidades.
Concluindo, calcular a soma dos elementos da diagonal secundária de uma matriz 3x3 em Python pode ser facilmente realizado com o uso de estruturas de controle simples e manipulação de listas. A abordagem envolve identificar corretamente os elementos da diagonal secundária e somá-los de maneira eficiente, garantindo que a matriz seja quadrada para aplicação correta do algoritmo. Com isso, você pode explorar e compreender melhor as propriedades das matrizes e a implementação de algoritmos em Python para tarefas específicas como esta.
FAQ
Matrizes são estruturas de dados compostas por linhas e colunas. Em Python, representamos matrizes com listas aninhadas.
A diagonal secundária de uma matriz 3×3 vai da primeira linha até a última coluna. Por exemplo, em uma matriz 3×3, a diagonal secundária é [2, 4, 6].
A NumPy é muito usada para trabalhar com matrizes em Python. Ela proporciona estruturas eficientes e funções avançadas.
Para criar uma matriz 3×3 em Python, usamos listas aninhadas. Por exemplo: matriz = [[1, 2, 3], [4, 5, 6], [7, 8, 9]].
O algoritmo soma os elementos da diagonal secundária. Esses elementos estão nas coordenadas (0, 2), (1, 1) e (2, 0).
A soma da diagonal secundária é útil em várias áreas. Ela ajuda na análise de imagens, dados e engenharia. Pode ser usada para detectar padrões e resolver problemas.
Testamos o algoritmo com diferentes tipos de matrizes. Isso inclui matrizes com números inteiros e decimais. Verificamos se os resultados estão corretos.
Uma recomendação é utilizar a NumPy para realizar operações de forma eficiente. Evite iterações desnecessárias. Use funções built-in do Python. E siga princípios de programação limpa.
Autor



