Sumário
Introdução
Eu sempre fui fascinado pela matemática e suas aplicações. Lembrei-me do meu primeiro contato com a álgebra linear. Foi incrível ver como as matrizes poderiam ser tão poderosas em várias áreas.
Compreendi a relevância de realizar a transposição de matrizes, o que alterou minha perspectiva sobre a matemática.
Você vai aprender a usar Python para trabalhar com matrizes transpostas. Vamos explorar os conceitos e suas aplicações. Prepare-se para explorar o mundo da álgebra linear!

Antes de começarmos temos que fala sobre a diferença na indexação.
A diferença na indexação entre a matemática (onde muitas vezes começamos a contar a partir de 1) e a programação (onde começamos a contar a partir de 0) é uma fonte comum de confusão para iniciantes na programação. Vamos explorar essa diferença e explicar como ela afeta o acesso aos elementos em uma matriz.
Matemática: Indexação começando por 1
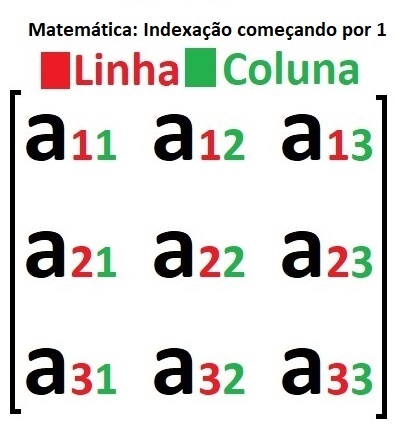
Na matemática e em muitas áreas de estudo acadêmico, como em álgebra linear e teoria dos grafos, é comum começar a contar a partir do número 1. Por exemplo, ao descrever uma matriz ou um sistema de coordenadas:
- Matriz: Os elementos são identificados com dois índices, onde o primeiro índice representa a linha e o segundo índice representa a coluna.
Em uma matriz 3x3, por exemplo, o elemento na primeira linha e primeira coluna é referido como (1,1), na segunda linha e segunda coluna é (2,2), e assim por diante.
Programação: Indexação começando por 0
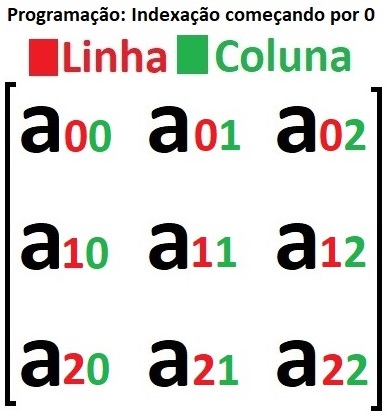
Por outro lado, na programação e na maioria das linguagens de programação, a indexação geralmente começa em 0. Isso significa que o primeiro elemento em uma lista, array ou matriz é acessado pelo índice 0, o segundo pelo índice 1, e assim por diante. Isso é especialmente comum em linguagens como Python, C, Java, JavaScript, entre outras.
Depois desse esclarecimento, vamos continuar!!
Principais aprendizados:
• Entender o que é uma matriz transposta e sua definição matemática.
• Aprender a criar e manipular matrizes transpostas usando a biblioteca NumPy do Python.
• Reconhecer as principais aplicações da transposição de matrizes é fundamental, particularmente em campos como álgebra linear e processamento de imagens.
• Aperfeiçoar habilidades em otimização de código para a transposição de matrizes é crucial.
• Explorar recursos adicionais e bibliotecas relevantes para operações matriciais em Python.
O que é uma matriz transposta?
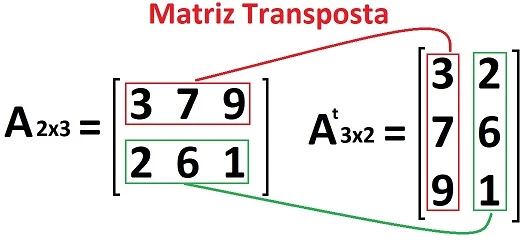
A matriz transposta é um conceito importante na álgebra linear e na programação científica. Ela é feita girando uma matriz original 90 graus. As linhas da matriz original viram colunas na matriz transposta. E as colunas viram linhas.
Definição e exemplos de matrizes transpostas
A matriz transposta de uma matriz A é representada por A^T. Cada elemento da matriz transposta vem da matriz original. Sua fórmula é:
(A^T)_{ij} = A_{ji}
Isso significa que o elemento na posição (i, j) da transposta é o mesmo que na posição (j, i) da original.
Por exemplo, a matriz A = [ 1 2 3 ; 4 5 6 ] tem sua transposta A^T assim:
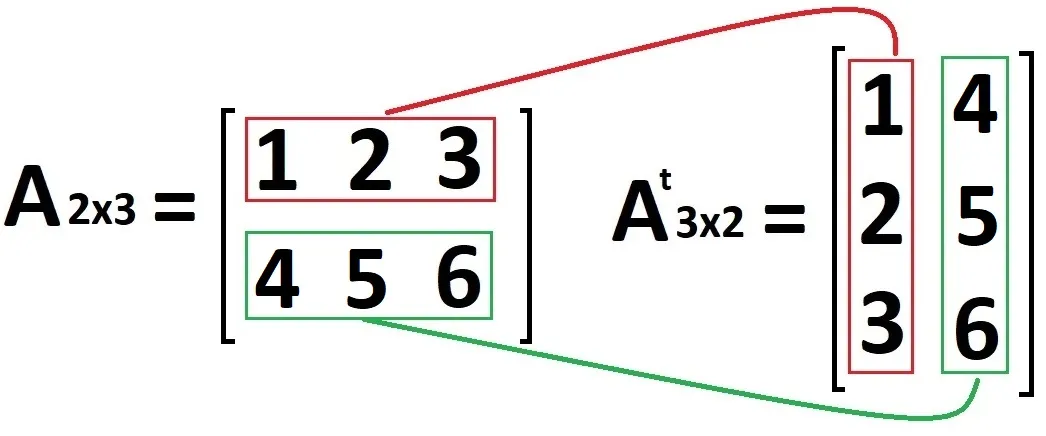
Importância da transposição de matrizes
A transposição de matrizes é crucial em várias áreas. Ela é usada na álgebra linear, no processamento de dados e na programação científica. Algumas aplicações importantes incluem:
• Cálculo de produtos matriciais e operações algébricas
• Análise de dados e transformações lineares
• Processamento de imagens e sinais
• Computação gráfica e visão computacional
Entender a matriz transposta é essencial para aplicar conceitos avançados da álgebra linear e da programação numérica.
Aplicações da transposição de matrizes
A transposição de matrizes é essencial em álgebra linear. Apresenta várias aplicações práticas na computação e na análise de dados. Vamos ver algumas dessas aplicações importantes.
Álgebra linear e operações matriciais
Na álgebra linear, a transposição de matrizes é crucial. Ela facilita operações matriciais, como a multiplicação de matrizes. Essa habilidade é vital em várias áreas, como resolver sistemas lineares e analisar transformações geométricas.
Processamento de imagens e sinais
As matrizes transpostas são essenciais no processamento de imagens e sinais. Elas são fundamentais na transformada de Fourier e na filtragem de dados. Isso ajuda na análise espectral de sinais e na criação de filtros lineares.
| Aplicação | Descrição |
|---|---|
| Álgebra linear | Operações matriciais, como multiplicação de matrizes |
| Processamento de imagens e sinais | Transformada de Fourier, filtragem de dados |
| Aprendizado de máquina | Decomposição de matrizes, redução de dimensionalidade |
| Análise de redes e grafos | Cálculo de métricas de centralidade, detecção de comunidades |
Essas são apenas algumas das muitas aplicações da transposição de matrizes. Vamos explorar mais casos de uso e técnicas avançadas envolvendo matrizes transpostas.

Por que usar Python para transpor matrizes?
A linguagem de programação Python é ótima para transpor matrizes. Possui uma sintaxe simples e conta com bibliotecas robustas, como o NumPy. Isso ajuda muito na manipulação de dados complexos, como matrizes.
Uma grande vantagem do Python é sua eficiência. Ela oferece eficiência e precisão em cálculos matemáticos e na manipulação de dados. Isso faz do Python uma escolha perfeita para trabalhar com processamento de dados numéricos.
• Sintaxe limpa e fácil de entender, facilitando a escrita e manutenção do código.
• Ampla gama de bibliotecas e pacotes disponíveis, como o NumPy, que oferecem funções prontas para transposição de matrizes.
• Eficiência na manipulação de estruturas de dados multidimensionais, como matrizes e arrays.
• Integração com outras ferramentas e bibliotecas populares, permitindo fluxos de trabalho mais robustos.
O Python também é multiplataforma. Isso significa que o código funciona em vários sistemas operacionais. Isso aumenta sua versatilidade e adoção em diferentes lugares.
Em conclusão, o Python é uma excelente escolha para transpor matrizes.Sua sintaxe clara, as bibliotecas disponíveis e a eficiência no processamento de dados são grandes benefícios. Sua popularidade e capacidade de se integrar com outras ferramentas fazem do Python uma ótima opção para quem busca soluções robustas e performáticas para matrizes.
Matriz transposta com Python
Para trabalhar com a transposição de matrizes em Python, vamos usar a biblioteca NumPy. Ela é muito usada para trabalhar com arrays e matrizes. Oferece muitas funcionalidades para fazer cálculos avançados.
Introdução ao NumPy
O NumPy cria uma estrutura de dados chamada ndarray (n-dimensional array). Isso facilita bastante o trabalho com arrays e matrizes. É muito usado em aprendizado de máquina, processamento de sinais e análise de dados.
Transposição de matrizes com NumPy
Com o NumPy, fazer a transposição de matrizes é simples e rápido. A função numpy.transpose() ou o atalho T inverte as linhas e colunas. Assim, a matriz muda para sua forma transposta.
Veja um exemplo prático:
import numpy as np
# Criando uma matriz 3x4
matriz = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
# Transpondo a matriz
matriz_transposta = matriz.T
print("Matriz original:")
print(matriz)
print("\nMatriz transposta:")
print(matriz_transposta)
Neste exemplo, a matriz original de 3x4 se torna uma matriz transposta de 4x3. Isso muda suas dimensões.
A transposição de matrizes é muito importante em álgebra linear. Tem muitas aplicações, como em processamento de imagens e análise de dados. Saber fazer isso com NumPy é essencial para quem trabalha com manipulação de arrays em Python e operações com matrizes em Python.
Aqui está o código completo que não usa biblioteca como o NumPy, para implementar transposição de matriz:
def obter_numero(mensagem):
while True:
try:
return int(input(mensagem))
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
def criar_matriz(num_linha, num_coluna):
matriz = []
for linha_numero in range(num_linha):
linha = []
for coluna_numero in range(num_coluna):
while True:
try:
valor = int(
input(f'\033[1;35mPor Favor, digite o {coluna_numero + 1}º elemento da {linha_numero + 1}º '
f'linha: \033[m'))
linha.append(valor)
break
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
matriz.append(linha)
return matriz
def gera_matriz_transposta(matriz, num_linhas, num_colunas):
return [[matriz[j][i] for j in range(num_linhas)] for i in range(num_colunas)]
def mostrar_matriz_gerada(matriz_gerada):
print()
for mostra_matriz in matriz_gerada:
print(f'\033[1;36m{mostra_matriz}\033[m')
print('\033[1;41m*** Inicializando o programa ***\033[m\n')
numero_linhas = obter_numero('\033[1;34mDigite o número de linhas da matriz: \033[m')
numero_colunas = obter_numero('\033[1;34mDigite o número de colunas da matriz: \033[m')
print()
matriz = criar_matriz(numero_linhas, numero_colunas)
print('\n\033[1;34mMatriz inserida:\033[m')
mostrar_matriz_gerada(matriz)
print()
print('\033[1;41m*** Matriz transposta ***\033[m\n')
matriz_transposta = gera_matriz_transposta(matriz, numero_linhas, numero_colunas)
for transposta2 in matriz_transposta:
print(f'\033[1;36m{transposta2}\033[m')
Este código Python realiza a criação de uma matriz, permite ao usuário inserir valores nela, e em seguida gera e exibe a matriz transposta.
Função `criar_matriz(num_linha, num_coluna)`:
- Esta função cria uma matriz com o número de linhas (`num_linha`) e colunas (`num_coluna`) especificados.
- Utiliza loops aninhados para percorrer cada linha e cada coluna da matriz.
A função gera_matriz_transposta(matriz, num_linhas, num_colunas)
- Retorna a matriz preenchida com os valores fornecidos pelo usuário.
cria a matriz transposta usando list comprehension. Neste caso, a transposição é feita trocando as linhas pelas colunas da matriz original, iterando através das colunas com o índice i e das linhas com o índice j.
Otimizando o código para transposição de matrizes
Trabalhar com operações com matrizes em Python exige foco na otimização do código. Isso é crucial para um bom desempenho. Vamos explorar técnicas que melhoram a performance em operações com matrizes, focando na transposição de matrizes.
Usar bibliotecas otimizadas para manipulação de matrizes é uma estratégia chave. O NumPy, por exemplo, oferece funções eficientes para a transposição de matrizes. Essas funções aproveitam recursos de baixo nível do Python para acelerar os cálculos.
Outra técnica interessante é a paralelização de tarefas. Dividir o processamento em múltiplos cores ou threads melhora a performance em matrizes grandes. Ferramentas como o Dask e o Numba ajudam a implementar essa técnica.
É essencial também seguir outras dicas de otimização em Python. Isso inclui usar estruturas de dados eficientes, evitar loops desnecessários e usar técnicas de memória compartilhada. Essas práticas melhoram muito o desempenho da transposição de matrizes.
Combinando essas estratégias, você alcançará resultados impressionantes na otimização de código para transposição de matrizes. Isso torna o trabalho mais fluido e produtivo.
Recursos adicionais e bibliotecas relevantes
Além do NumPy, existem outras bibliotecas Python que ajudam muito na manipulação de matrizes. A Pandas é uma delas. Ela traz funcionalidades avançadas para trabalhar com dados estruturados.
Pandas e outras bibliotecas úteis
A Pandas é muito usada para lidar com dados. Isso inclui carregar e transpor matrizes. Ela também permite fazer várias operações matemáticas e estatísticas.
Outras bibliotecas importantes para trabalhar com matrizes em Python são:
• SciPy: oferece diversas funções matemáticas e científicas, incluindo operações com matrizes.
• Matplotlib: Ajuda a visualizar dados, mostrando matrizes transpostas de forma gráfica.
• Sympy: Permite trabalhar com expressões simbólicas, incluindo matrizes.
Escolher a biblioteca certa é crucial. Cada uma tem suas particularidades. É importante conhecer bem cada uma para obter os melhores resultados na transposição de matrizes.

Dicas e melhores práticas
Trabalhar com matrizes transpostas em Python pode ser mais fácil com algumas dicas. Aqui estão algumas recomendações para melhorar seu código. Elas ajudam a tornar seu trabalho mais eficiente e simples de manter.
1. Use a biblioteca NumPy: O NumPy oferece métodos fáceis para transpor matrizes. Use np.transpose() ou matriz.T. Isso evita a necessidade de fazer tudo manualmente.
2. Adote boas práticas de programação: Siga as melhores práticas em python. Nomeie variáveis e funções de forma clara. Use docstrings para documentar seu código. E aplique testes unitários para verificar se tudo está correto.
3. Otimize o desempenho: Use técnicas de programação eficiente para melhorar seu código. Evite loops aninhados sempre que possível. E aproveite a paralelização do NumPy.
4. Gerencie erros e exceções: Lide com erros e exceções de maneira apropriada. Verifique o formato das matrizes antes de transpor.
5. Documente seu código: Adicione comentários explicativos. E forneça exemplos de uso. Isso torna seu código mais legível e fácil de manter.
Seguindo essas dicas e melhores práticas, você criará soluções de transposição de matrizes em Python melhores. Elas serão mais robustas, eficientes e fáceis de entender e manter.
Desafios comuns ao transpor matrizes
Trabalhar com a transposição de matrizes em Python pode ser desafiador. Mas, com a preparação certa, você pode superá-los facilmente. Vamos explorar os erros comuns em operações com matrizes e as soluções para problemas com matrizes transpostas.
Dimensões incompatíveis
Um grande desafio é lidar com dimensões incompatíveis. Isso acontece quando tentamos operar matrizes de tamanhos diferentes. É crucial verificar as dimensões das matrizes antes de operar.
• Use a função numpy.shape() para ver as dimensões da matriz.
• Verifique se as matrizes têm as mesmas dimensões antes da transposição.
• Se necessário, ajuste o tamanho das matrizes antes da transposição.
Erros de indexação
Outro desafio comum é lidar com erros de indexação. Isso ocorre quando não entendemos como as matrizes são armazenadas e indexadas em Python.
1. Tenha em mente que a indexação em Python inicia a contagem a partir de 0. O primeiro elemento está no índice 0,0.
2. Atenção à ordem dos índices: linha, coluna.
3. Use a documentação do NumPy para entender melhor a indexação.
Enfrentando esses desafios na transposição de matrizes, use o troubleshooting em python. Isso simplifica a identificação e a correção de problemas.
Com o conhecimento adquirido, você estará pronto para enfrentar erros e soluções típicas ao trabalhar com a transposição de matrizes em seus projetos.
Casos de uso avançados
Exploraremos casos de uso avançados da transposição de matrizes em Python. Vamos ver como ela é essencial em análise de dados, aprendizado de máquina e simulações científicas.
A transposição de matrizes é crucial na álgebra linear aplicada. Ela permite operações matemáticas complexas. Por exemplo, a decomposição de valores singulares (SVD) é vital para redução de dimensionalidade e aprendizado de máquina.
Na área de processamento de imagens e sinais, a transposição é crucial. Ela permite realizar transformações geométricas, como rotação e reflexão. Essas transformações são essenciais para reconhecimento de padrões e filtragem de imagens.
Além disso, a transposição é usada em simulações científicas e de engenharia. Modelos matemáticos complexos, como equações diferenciais parciais, são representados e resolvidos de forma eficiente com matrizes transpostas.
Com habilidade em técnicas de manipulação de matrizes avançadas, você pode explorar diversas aplicações complexas em Python. Isso expande seus casos de uso avançados para matrizes transpostas.
"A transposição de matrizes é uma ferramenta valiosa que capacita cientistas e engenheiros a resolver problemas cada vez mais complexos."
| Aplicação | Descrição | Benefícios da transposição de matrizes |
|---|---|---|
| Álgebra linear aplicada | Decomposição de valores singulares (SVD), redução de dimensionalidade, aprendizado de máquina | Permite realizar operações matemáticas mais complexas e extrair informações relevantes |
| Processamento de imagens e sinais | Transformações geométricas, reconhecimento de padrões, filtragem de imagens | Facilita a aplicação de operações lineares em dados multidimensionais |
| Simulações científicas e de engenharia | Modelos matemáticos complexos, equações diferenciais parciais | Proporciona uma representação eficiente e permite a resolução de problemas matemáticos avançados |
Conclusão
Exploramos a transposição de matrizes em Python neste artigo. Vimos que transpor uma matriz é simples, mas muito útil. Isso vale para a álgebra linear e para muitas aplicações, como processamento de imagens.
Usamos a biblioteca NumPy para fazer isso de forma eficiente. Entendemos como essa operação é crucial em cálculos matriciais e análise de dados. Também falamos sobre como otimizar o código para trabalhar com grandes matrizes.
Com esse conhecimento, sugiro que você explore mais recursos, como Pandas e Scipy. Isso contribuirá para uma compreensão mais profunda da transposição de matrizes em Python. Praticar regularmente é essencial para fixar esses conhecimentos.
FAQ
Uma matriz transposta é feita trocando as linhas e colunas de uma matriz original. Os elementos da linha i da matriz original ficam na coluna i da matriz transposta.
Ela é fundamental na álgebra linear e possui várias aplicações, como operações matriciais, processamento de imagens e análise de dados.
Python é ótimo para trabalhar com matrizes devido à sua facilidade. Tem bibliotecas como o NumPy que ajudam muito.
Com o NumPy, pode-se utilizar a função `np.transpose()` ou o operador `T` para realizar a transposição de matrizes. Basta aplicar essa função a um array NumPy para obter a matriz transposta.
Ela é usada em várias áreas. Por exemplo, na álgebra linear e no processamento de imagens e sinais.
Para otimizar, use eficientemente bibliotecas como o NumPy. Também pode-se paralelizar tarefas para melhorar o desempenho.
Além do NumPy, a Pandas também ajuda muito. Existem outras bibliotecas que podem atender às suas necessidades.
Desafios comuns são erros de dimensões. Para resolver, use técnicas de depuração e otimização. Boas práticas envolvem uma sintaxe clara e técnicas para otimizar o desempenho.
Sim, é aplicada em análise de dados, aprendizado de máquina e simulações científicas. Essas aplicações exigem técnicas avançadas.
Autor