Sumário
Multiplicação de matrizes, mas antes de começarmos ter que fala sobre a diferença na indexação.
A diferença na indexação entre a matemática (onde muitas vezes começamos a contar a partir de 1) e a programação (onde começamos a contar a partir de 0) é uma fonte comum de confusão para iniciantes na programação. Vamos explorar essa diferença e explicar como ela afeta o acesso aos elementos em uma matriz.
Matemática: Indexação começando por 1
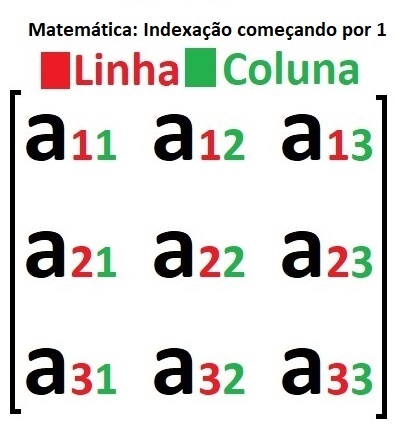
Na matemática e em muitas áreas de estudo acadêmico, como em álgebra linear e teoria dos grafos, é comum começar a contar a partir do número 1. Por exemplo, ao descrever uma matriz ou um sistema de coordenadas:
- Matriz: Os elementos são identificados com dois índices, onde o primeiro índice representa a linha e o segundo índice representa a coluna.
Em uma matriz 3x3, por exemplo, o elemento na primeira linha e primeira coluna é referido como (1,1), na segunda linha e segunda coluna é (2,2), e assim por diante.
Programação: Indexação começando por 0
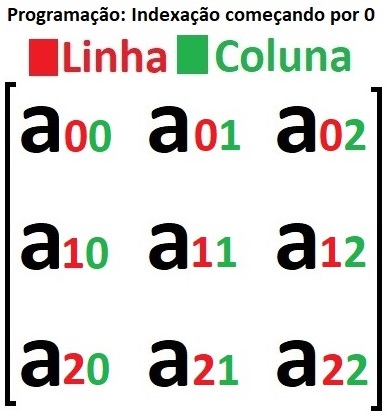
Por outro lado, na programação e na maioria das linguagens de programação, a indexação geralmente começa em 0. Isso significa que o primeiro elemento em uma lista, array ou matriz é acessado pelo índice 0, o segundo pelo índice 1, e assim por diante. Isso é especialmente comum em linguagens como Python, C, Java, JavaScript, entre outras.
Depois desse esclarecimento, vamos continuar!!
A multiplicação de matrizes em Python pode parecer difícil no começo. Mas com este guia, você vai aprender tudo que precisa saber. Isso é essencial para áreas como ciências de dados, machine learning e matemática aplicada.
Python é fácil de usar e muito poderoso. Ele tem bibliotecas como NumPy que tornam a manipulação de matrizes muito simples. Este artigo é para iniciantes e para quem já conhece outras linguagens.

Principais Pontos.
• Entenda o conceito de multiplicação de matrizes
• Descubra como construir e trabalhar com matrizes em Python
• Investigue como utilizar a biblioteca NumPy para trabalhar com matrizes
• Veja exemplos práticos de multiplicação de matrizes em Python
• Compreenda a importância de matrizes em diversas aplicações práticas
Introdução à Multiplicação de Matrizes.
Antes de mergulharmos na multiplicação de matrizes, é crucial entender o que são e como são usadas. Matrizes são ferramentas poderosas na matemática e na programação. Elas são essenciais para lidar com grandes volumes de dados.
O que São Matrizes?
Matrizes são arrays bidimensionais com elementos em linhas e colunas. Em Python, usamos bibliotecas como NumPy para trabalhar com elas. Saber trabalhar com matrizes em Python é essencial para áreas como álgebra linear e processamento de sinal.
Aplicações Práticas das Matrizes.
As matrizes têm muitas aplicações práticas. Por exemplo:
• Computação Gráfica: Elas são usadas para transformações e rotações de imagens.
• Física: Matrizes ajudam a resolver equações diferenciais que modelam fenômenos físicos.
• Engenharia: Elas são importantes na análise de estruturas e redes elétricas.
• Ciência de Dados: Matrizes são usadas para manipular e analisar grandes conjuntos de dados.
Essas aplicações mostram a importância das matrizes em várias disciplinas. Conhecer matrizes em Python pode abrir muitas portas para carreiras.
Conceitos Básicos de Matrizes em Python.
Vamos explorar conceitos fundamentais para trabalhar com matrizes. Python é uma linguagem poderosa para criar e manipular matrizes. Entender como lidar com matrizes em Python é crucial para um algoritmo de multiplicação de matrizes bem-sucedido.
Como Criar Matrizes no Python.
Para criar matrizes python, usamos listas aninhadas. Por exemplo, uma matriz 2x2 pode ser representada da seguinte maneira:
matriz = [[1, 2],[3, 4]]
Com essa estrutura, acessamos elementos usando índices. Para obter o primeiro elemento da segunda linha, utilizamos:
elemento = matriz[1][0]
Lendo e Escrevendo Matrizes.
A leitura e escrita de elementos em matrizes Python são simples. Modificamos valores acessando o índice desejado. Por exemplo, para alterar o valor da posição [0][1], fazemos:
matriz[0][1] = 5
Podemos iterar por todos os elementos de uma matriz com laços de repetição:
matriz = [[1, 2], [3, 4]]
for linha in matriz:
for elemento in linha:
print(elemento)
Essas técnicas ajudam a manipular e visualizar matrizes. Elas facilitam a implementação do seu algoritmo de multiplicação de matrizes.
Multiplicação de Matrizes fazendo uso da linguagem de programação Python.
A multiplicação de matrizes python é crucial no desenvolvimento de software. Isso é particularmente relevante para áreas como ciência de dados, aprendizado de máquina e computação gráfica. Vou mostrar como Python facilita essa tarefa e suas vantagens.
Python torna a multiplicação de matrizes muito simples. A NumPy é a biblioteca mais utilizada para isso. Ela permite fazer operações complexas com matrizes rapidamente.
Na prática, a multiplicação de matrizes em Python é extremamente valiosa. Ela é executada em diversas áreas, como:
• Simulações científicas: para processar grandes quantidades de dados.
• Análise de dados: para manipular e transformar conjuntos de dados em larga escala.
• Desenvolvimento de algoritmos de aprendizado de máquina: onde matrizes são essenciais.
Aqui vai um exemplo simples de uso:
import numpy as np
# Definindo duas matrizes
matriz_A = np.array([[1, 2], [3, 4]])
matriz_B = np.array([[5, 6], [7, 8]])
# Multiplicação de matrizes utilizando NumPy
resultado = np.dot(matriz_A, matriz_B)
print(resultado)
Com poucas linhas de código, a multiplicação de matrizes python fica simples. Isso mostra a flexibilidade e força da linguagem Python, especialmente com a NumPy.
Passos para a Implementação da Multiplicação de Matrizes.
Para fazer a multiplicação de matrizes em Python, é importante configurar o ambiente certo. Também é essencial usar as bibliotecas certas. Vamos ver os passos para você estar pronto para isso.
Passo 1: Configuração do Ambiente Python.
A configuração do ambiente Python é o primeiro passo. Faça uma avaliação se o programa do Python está instalado no seu computador. É bom usar a versão mais nova para trabalhar com as últimas bibliotecas.
Além disso, pense em usar um ambiente virtual. Isso auxilia na gestão das dependências do seu projeto.
Veja os comandos básicos que você vai precisar:
Se estiver usando o sistema operacional Linux use o comando 'sudo apt-get install', se for Windows tem que abaixar instalador.
1. Instalar o Python: sudo apt-get install python3
2. Configurar um ambiente virtual: python3 -m venv myenv (Tanto Linux quanto Windows)
3. Ativar o ambiente virtual: source myenv/bin/activate (Usado no Linux)
Para ativar o ambiente virtual no Windows usando o prompt de comando CMD:
.\venv\Scripts\activate.bat
Usando o PowerShell:
.\venv\Scripts\activate.ps1
Se receber uma mensagem de erro talvez tenha que usar este comando no prompt de comando do PowerShell:
Set-ExecutionPolicy -Scope CurrentUser -ExecutionPolicy RemoteSigned

Passo 2: Biblioteca NumPy.
Com o Python configurado, o próximo passo é usar a biblioteca NumPy. NumPy é fundamental para lidar com vetores e matrizes na computação científica.
Para instalar o NumPy, use o comando:
pip install numpy
Depois de instalar, você pode começar a usar o NumPy em seu código. Veja um exemplo simples de multiplicação de matrizes:
import numpy as np
matrizA = np.array([[1, 2], [3, 4]])
matrizB = np.array([[5, 6], [7, 8]])
resultado = np.dot(matrizA, matrizB)
print(resultado)
Com esses passos, você está pronto para aprender mais sobre a multiplicação de matrizes em Python. E também sobre como usar o NumPy para resolver problemas complexos.
Exemplo Prático de Multiplicação de Matrizes.
Vamos ver como multiplicar matrizes em Python. Primeiro, definimos dois arrays. Depois, mostramos como multiplicá-los usando técnicas básicas da linguagem.
Definindo as Matrizes.
Primeiro, definimos as matrizes que vamos usar. Veja um exemplo de multiplicação de matrizes:
A = [[1, 2],[3, 4]]
B = [[5, 6],[7, 8]]
A matriz A é uma matriz 2x2, assim como a matriz B. Agora, podemos começar a multiplicação.
Realizando a Multiplicação.
Para multiplicar as matrizes, usamos Python. Veja como fazer isso:
import numpy as np
A = np.array([[1, 2],[3,4]])
B = np.array([[5, 6],[7,8]])
resultado = np.dot(A, B)
print(resultado)
O resultado dessa operação é:
[[19 22]
[43 50]]
Esse exemplo mostra como fazer multiplicação de matrizes simplesmente em Python. Usamos NumPy para facilitar e aumentar a precisão.
A tabela abaixo resume as operações feitas:
| Elemento | Cálculo | Resultado |
|---|---|---|
| Elemento [1,1] | (1\*5) + (2\*7) | 19 |
| Elemento [1,2] | (1\*6) + (2\*8) | 22 |
| Elemento [2,1] | (3\*5) + (4\*7) | 43 |
| Elemento [2,2] | (3\*6) + (4\*8) | 50 |
Esse exemplo mostra como fazer multiplicação de matrizes de forma eficaz em Python. Com esses conceitos, você estará pronto para problemas mais complexos.

| Operação | Descrição | Exemplo |
|---|---|---|
| Validar Dimensões | Verifica se as matrizes podem ser multiplicadas | A: 2x3, B: 3x2. Pode! |
| Inicializar Matriz C | Matriz de zeros com dimensões de resultado | [[0, 0], [0, 0]] |
| Multiplicar e Somar | Soma dos produtos correspondentes de A e B | [[19, 22], [43, 50]] |
Código complexo em Python sem uso de biblioteca.
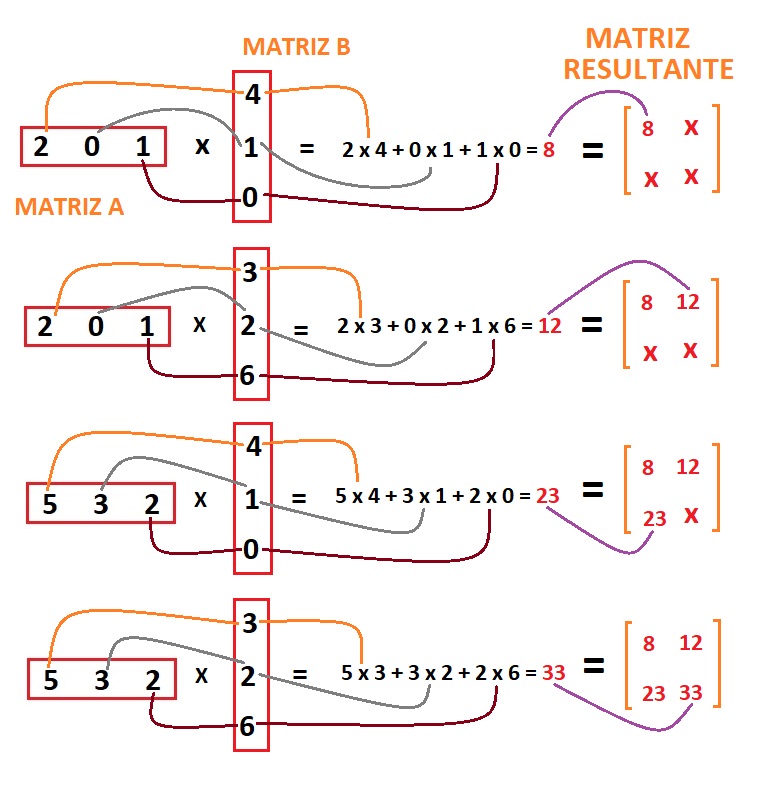
Para multiplicar duas matrizes precisam ser quadradas? Nada disso!
Não necessariamente as duas precisam ser da mesma ordem, mas precisa de uma condição.
"O número de colunas da primeira matriz deve ser igual ao número de linhas da segunda matriz para que a multiplicação de matrizes seja possível."
E agora: A matriz resultante vai ser exatamente os números de fora.
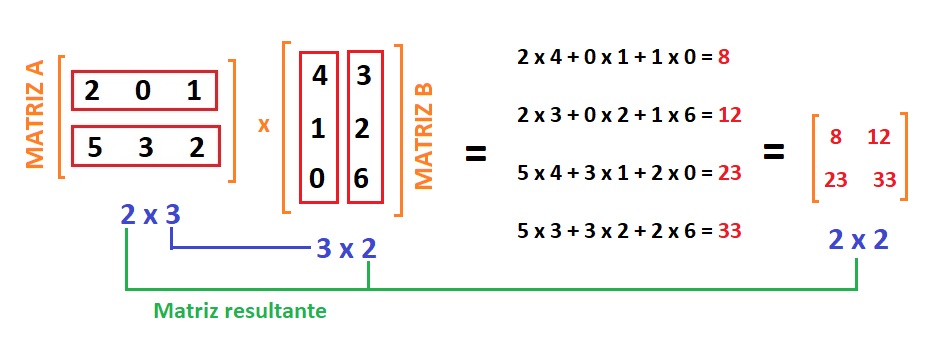
Detalhe da resolução:
Código-fonte do programa em Python.
import sys
def checkMatriz(colunaMatrizA, linhaMatrizB):
# print(colunaMatrizA, linhaMatrizB)
if int(colunaMatrizA) != int(linhaMatrizB):
print(f'\033[1;31mErro: As dimensões das matrizes não são compatíveis para multiplicação.\033[m')
print(f'\033[1;91mPrograma Finalizado!!!!!!.\033[m')
return sys.exit()
else:
print()
print(f'\033[1;96mAs dimensões das matrizes são compatíveis para multiplicação. '
f'\nVamos continuar!!!!!.\033[m')
print()
return
def criar_matriz(num_linhas, num_colunas):
matriz = []
for i in range(num_linhas):
linha = []
for j in range(num_colunas):
while True:
try:
valor = int(input(f'Digite o {j + 1}º elemento da {i + 1}ª linha: '))
linha.append(valor)
break
except ValueError:
print(f'\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
matriz.append(linha)
return matriz
def getLinha(matriz, n):
return [i for i in matriz[n]]
def getColuna(matriz, n):
return [i[n] for i in matriz]
print(f'\033[1;34mIniciando o programa de multiplicação de matrizes.\033[m')
print(f'\033[1;33mDeterminando as ordens das matrizes.\033[m')
print(f'\033[1;33mPrimeira Matriz.\033[m')
while True:
try:
numero_linhas_1 = int(input('Digite o número de linhas da matriz: '))
numero_colunas_1 = int(input('Digite o número de colunas da matriz: '))
break
except ValueError:
print(f'\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
print()
print(f'\033[1;33mSegunda Matriz.\033[m')
while True:
try:
numero_linhas_2 = int(input('Digite o número de linhas da matriz: '))
numero_colunas_2 = int(input('Digite o número de colunas da matriz: '))
break
except ValueError:
print(f'\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
checkMatriz(numero_colunas_1, numero_linhas_2)
print(f'\033[1;33mCriando a primeira Matriz.\033[m')
matriz_A = criar_matriz(numero_linhas_1, numero_colunas_1)
print()
print(f'\033[1;33mCriando a segunda Matriz.\033[m')
matriz_B = criar_matriz(numero_linhas_2, numero_colunas_2)
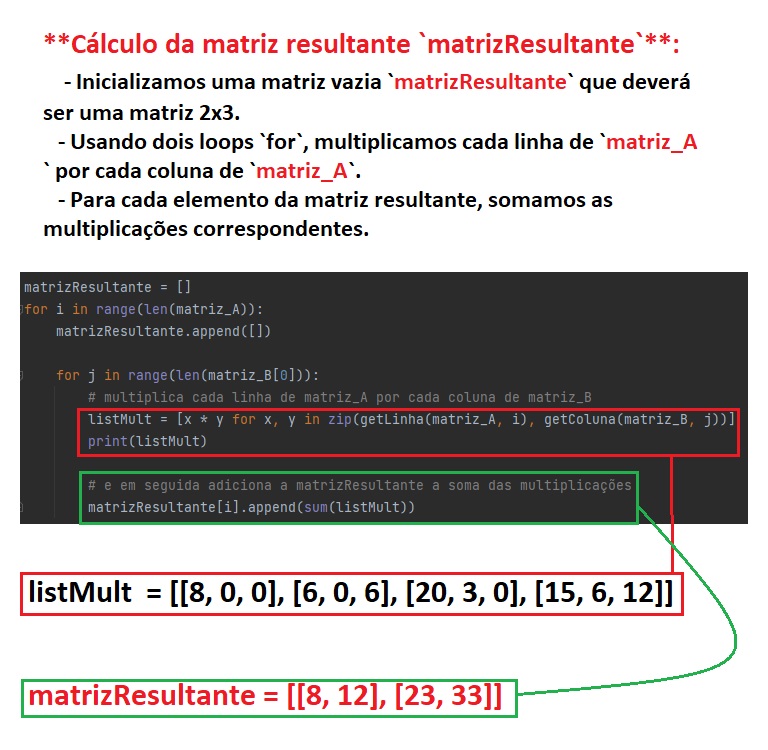
matrizResultante = []
for i in range(len(matriz_A)):
matrizResultante.append([])
for j in range(len(matriz_B[0])):
print(f'getLinha(matriz_A, i): {getLinha(matriz_A, i)}')
print(f'getColuna(matriz_B, j): {getColuna(matriz_B, j)}')
# multiplica cada linha de matriz_A por cada coluna de matriz_B
listMult = [x * y for x, y in zip(getLinha(matriz_A, i), getColuna(matriz_B, j))]
# print(listMult)
# e em seguida adiciona a matrizResultante a soma das multiplicações
matrizResultante[i].append(sum(listMult))
# Print results.
print()
print("\033[1;31mMatriz original A\033[m")
for linha in matriz_A:
print(linha)
print()
print("\033[1;31mMatriz original B\033[m")
for linha in matriz_B:
print(linha)
print()
print(f'\033[1;33mO Resulto da multiplicação das matrizes:\033[m')
for linha in matrizResultante:
print(f'\033[1;31m{linha}\033[m')
Estamos usando a função zip em Python para combinar listas.
A função zip em Python é uma ferramenta altamente vantajosa para combinar listas. Ela possibilita agrupar elementos de várias listas em tuplas, formando uma nova lista combinada. Essa funcionalidade é essencial em diversas situações, desde o processamento de dados até o desenvolvimento de algoritmos sofisticados, facilitando a manipulação coordenada de informações entre diferentes conjuntos de dados ou estruturas de dados.
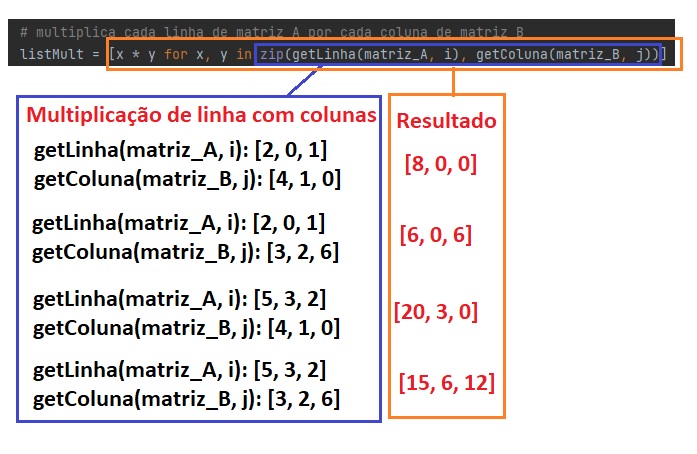
Definição das funções `getLinha` e `getColuna`:
- A função `getLinha(matriz, n)` retorna uma lista com os valores da linha `n` da matriz.
- A função `getColuna(matriz, n)` retorna uma lista com os valores da coluna `n` da matriz.
A função `zip` combina os elementos correspondentes das duas listas.
- `getLinha(matriz_A, i)` retorna a linha `i` de ` matriz_A `.
- `getColuna(matriz_B, j)` retorna a coluna `j` de ` matriz_A `.
Programação em Python para Matrizes.
A programação em python para matrizes é muito versátil. Ela vai desde operações simples até técnicas avançadas. Vamos ver funções e métodos úteis para trabalhar com matrizes em Python.
Funções Utilitárias para Matrizes.
Python tem várias funções utilitárias para matrizes. Elas ajudam muito nas operações comuns. Algumas das mais usadas são:
• numpy.zeros: Cria uma matriz de zeros.
• numpy.ones: Cria uma matriz de uns.
• numpy.eye: Cria uma matriz identidade.
• numpy.dot: Realiza a multiplicação de matrizes.
Essas funções são cruciais para quem trabalha com matrizes em Python.
Manipulação Avançada de Matrizes.
A manipulação avançada de matrizes facilita operações complexas. A biblioteca NumPy oferece métodos para transposição, inversão e decomposição de matrizes.
Algumas técnicas avançadas são:
1. Matriz Transposta: Com numpy.transpose, obtem-se a transposta de uma matriz.
2. Inversão de Matrizes: numpy.linalg.inv calcula a inversa de uma matriz.
3. Decomposição LU: scipy.linalg.lu decompe uma matriz em fatores.
Com essas técnicas, a programação em python para matrizes se torna muito mais eficaz. Ela é essencial em ciência de dados, engenharia e outras áreas.
Manipulação de Matrizes com NumPy.
Explorar a manipulação de matrizes python com NumPy é muito enriquecedor. A biblioteca NumPy traz muitas funcionalidades. Ela permite fazer operações matemáticas e lógicas com facilidade. Se você já sabe um pouco de python ou está começando, vai se surpreender com o que pode fazer.

Usar NumPy para trabalhar com matrizes é muito fácil. Veja algumas das principais funcionalidades:
• Criação e manipulação de arrays multidimensionais.
• Operações de álgebra linear, como multiplicação de matrizes, são simples.
• Tem funções para operações matemáticas avançadas.
• Além disso, oferece ferramentas de análise estatística.
Para mostrar como é fácil, vamos ver alguns exemplos com NumPy:
| Função | Descrição | Exemplo de Código |
|---|---|---|
| np.dot | Multiplicação de matrizes | np.dot(a, b) |
| np.linalg.inv | Inversão de matriz | np.linalg.inv(a) |
| np.sum | Soma dos elementos | np.sum(a) |
| Table Data | np.mean | np.mean(a) |
| np.transpose | Transposição de matriz | np.transpose(a) |
Com essas ferramentas, fica claro como NumPy facilita o trabalho com matrizes. Ela torna a programação eficiente e precisa. Isso ajuda a obter resultados rápidos e exatos.
Multiplicação de Matrizes Python Passo a Passo.
Vamos explorar a multiplicação de matrizes em Python. Isso é fundamental para áreas como ciência de dados e engenharia. Entender como fazer isso passo a passo é crucial.
Implementação Manual.
Para multiplicar matrizes manualmente, precisamos seguir alguns passos. Imagine que temos matrizes A e B para multiplicar.
1. Faça uma verificação se o número de colunas de A é igual ao número de linhas de B.
2. Faça uma matriz que tenha como resultado com número de linhas da matriz A e o número de colunas da matriz B.
3. Calcular o produto ponto a ponto e armazenar na matriz de resultado.
Veja um exemplo de código para fazer isso:
def multiplicar_matrizes(a, b):
resultado = [[0 for col in range(len(b[0]))] for row in range(len(a))]
for i in range(len(a)):
for j in range(len(b[0])):
for k in range(len(b)):
resultado[i][j] += a[i][k] * b[k][j]
return resultado
A = [[1, 2], [3, 4]]
B = [[5, 6], [7, 8]]
print(multiplicar_matrizes(A, B))
Uso de Bibliotecas.
Para tornar a multiplicação mais fácil, usamos bibliotecas como o NumPy. O NumPy facilita muito a manipulação de matrizes.
Veja um exemplo com NumPy:
import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
resultado = np.dot(a, b)
print(resultado)
Exemplo com matrizes maiores.
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
B = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
# Realizando a Multiplicação:
C = np.dot(A, B)
print(C)
# O resultado será:
# [[ 30 24 18] [ 84 69 54] [138 114 90]]
Comparando, o NumPy é mais rápido e menos propenso a erros que fazer manualmente.
| Implementação | Vantagens | Desvantagens |
|---|---|---|
| Manual | Maior controle sobre cada passo | Mais suscetível a erros |
| Uso de bibliotecas python (NumPy) | Mais eficiente e menos código | Menos controle sobre o processo |
Python e Matrizes Multidimensionais.
Explorar matrizes em Python pode parecer um desafio. Mas, com prática, você verá sua força. Vamos ver os tipos de matrizes e como usá-las em Python para resolver problemas complexos.
Diferentes Tipos de Matrizes.
Python oferece vários tipos de matrizes. Cada um tem suas características e usos.
• Matrizes Unidimensionais: São as mais simples, conhecidas como vetores.
• Matrizes Bidimensionais: São como tabelas ou planilhas, para dados em linhas e colunas.
• Matrizes Tridimensionais: Representam dados em um espaço tridimensional, como cores em uma imagem RGB.
• Matrizes de N-Dimensões: Podem ter várias dimensões, usadas em aprendizado de máquina e processamento de sinais.
Para qualquer problema, provavelmente existe um tipo de matriz apropriado.
Usos de Matrizes Multidimensionais.
Matrizes multidimensionais são usadas em várias áreas da programação. Aqui estão alguns exemplos práticos:
• Processamento de Imagens: São usadas para manipular pixels e aplicar filtros.
• Simulações Científicas: Modelos matemáticos complexos são implementados com elas.
• Redes Neurais: Guardam pesos e saídas das camadas dos neurônios.
• Pesquisa Operacional: Ajudam a otimizar processos e resolver problemas complexos de programação linear.
Assim, vemos que matrizes multidimensionais em Python são flexíveis e muito úteis em muitas áreas.
Dicas de Depuração e Testes de Código de Matrizes.
Descobrir e resolver erros são partes essenciais do desenvolvimento de software. É crucial ter um código limpo, especialmente com operações complexas. Vou mostrar dicas práticas sobre depuração em python e testes de código python para matrizes.
Como Encontrar Erros Comuns.
Encontrar erros em um programa Python pode ser um desafio. Mas com a técnica certa, podemos simplificar muito esse processo. Aqui estão alguns passos para localizar e corrigir problemas frequentes:
• Verifique os índices: Certifique-se de que você não está acessando índices fora dos limites das matrizes.
• Confirme o tamanho das matrizes: As dimensões das matrizes devem ser compatíveis para multiplicação.
• Implemente logs detalhados: Adicione mensagens de log para entender melhor onde o erro ocorre.
Testando Seu Código.
Testar seu código de multiplicação de matrizes é essencial. Isso garante resultados exatos e desempenho eficiente. Aqui estão algumas práticas recomendadas para testes de código python:
1. Testes Unitários: Crie testes unitários para cada função envolvida na operação de multiplicação de matrizes.
2. Casos de Teste Diversos: Use vários casos de teste, incluindo matrizes de diferentes tamanhos e valores.
3. Avaliação de Desempenho: Teste o desempenho do seu código com matrizes grandes para garantir eficiência.
Investir tempo na depuração em python e fazer testes de código python eficazes ajuda muito. Assim, você evita problemas futuros. Isso garante que seu programa de multiplicação de matrizes funcione corretamente e eficientemente.
Conclusão:
Chegamos ao fim desta jornada sobre a multiplicação de matrizes em Python. Percorremos desde os conceitos fundamentais até a aplicação prática. Abordamos o que são matrizes e suas utilizações no mundo real.
Analisamos como criar e manipular matrizes usando a biblioteca NumPy. Também vimos exemplos práticos. Além disso, falamos sobre algoritmos e métodos de depuração para códigos precisos.
A multiplicação de matrizes é uma operação fundamental na álgebra linear, amplamente utilizada em diversas áreas da matemática e ciências aplicadas. Ao contrário da simples adição ou subtração de matrizes, que envolve operar elementos correspondentes, a multiplicação de matrizes segue regras específicas.
Neste processo, cada elemento de uma linha da primeira matriz é multiplicado pelos elementos correspondentes das colunas da segunda matriz, sendo que o resultado é um novo elemento na matriz resultante. Essa técnica é essencial em aplicações que envolvem transformações lineares, resolução de sistemas de equações lineares e na representação de dados em computação gráfica e processamento de imagens.
Foi criado um código na unha que necessita de vários conhecimentos básicos na linguagem python este tipo de problema nos força a evoluir (pensar) em como resolvê-lo usando IF, FOR, WHILE, zip(), range() o base da linguagem, poderia usar uma bala de prata para solucionar o problema com o NumPy (np.array) que pode ser usado em um ambiente de produção, agora quando somos estudantes e melhor é quebrar a cabeça que no final é gratificante.
Desejo que essas informações tenham utilidade para você. Aprender sobre matrizes em Python é essencial para resolver problemas complexos. Continue desenvolvendo suas habilidades em Python e enfrentando novos desafios!
FAQ
Matrizes são estruturas de dados que têm linhas e colunas. Elas são usadas para organizar e manipular dados. São relevantes tanto na matemática quanto na programação.
Matrizes são usadas em muitos lugares. Por exemplo, na computação gráfica, física, engenharia, ciência de dados e inteligência artificial. Elas ajudam a resolver problemas complexos.
Para criar matrizes no Python, você pode usar listas aninhadas. Ou então a biblioteca NumPy, que é mais eficiente e tem funções avançadas.
NumPy é essencial para trabalhar com matrizes no Python. Fornece suporte a arrays multidimensionais e uma variedade de funções matemáticas. É crucial para operações complexas.
Para multiplicar matrizes no Python, você pode usar loops ou a função dot da NumPy. A função dot faz o processo ser mais simples e rápido.
Primeiro, instale o Python em sua máquina. Depois, configure um ambiente de desenvolvimento, como o Jupyter Notebook ou PyCharm. Por fim, instale a NumPy com pip install numpy.
Primeiro, defina as matrizes que você quer multiplicar. Em seguida, use loops aninhados ou a função numpy.dot() para fazer a multiplicação. NumPy torna o código mais simples e eficiente.
Matrizes multidimensionais são usadas para dados complexos. Por exemplo, em imagens, transformações lineares e simulações científicas. Elas representam dados volumétricos.
Erros comuns incluem problemas de dimensões para multiplicação e indexação errada. Usar NumPy pode ajudar a evitar esses erros.
Utilize assertivas e condições para garantir que o código esteja funcionando corretamente. Ferramentas como unittest do Python ou bibliotecas de depuração em IDEs podem ajudar a encontrar e corrigir erros.
Autor

Robson Guedes Ferreira
Gosto de programação, eletrônica e games, sempre quis escrever sobre este assunto, espero que ajude alguém!!!!!


