Sumário
A humanidade sempre se encantou com os padrões encontrados na natureza, e a Sequência de Fibonacci é um exemplo fascinante disso. Ela mostra uma lógica e beleza que impressionam, com usos em arquitetura, design e biologia.
Este artigo vai explorar a Sequência de Fibonacci. Vamos descobrir seus segredos e como ela aparece na natureza. Veremos espirais de conchas, simetrias de girassóis e mais, mostrando como ela é um dos "números mágicos" da natureza.
Principais Destaques.
• A Sequência de Fibonacci revela padrões numéricos incríveis na natureza
• Essa série numérica se manifesta em espirais, simetrias e arranjos de elementos naturais
• Entender a Sequência de Fibonacci nos ajuda a compreender melhor a matemática por trás dos fenômenos naturais
• As aplicações práticas dessa sequência vão desde a arquitetura até o design, passando pela arte e cultura
• A Razão Áurea, uma proporção fundamental na natureza, está intimamente ligada à Sequência de Fibonacci
O que é a Sequência de Fibonacci?
A sequência de Fibonacci é uma série numérica que mostra padrões incríveis. Começa com 0 e 1, e cada número é a soma dos dois anteriores. Assim, ela cresce exponencialmente, formando uma sequência de números.
Descobrindo os padrões numéricos.
A sequência de Fibonacci não é apenas uma sequência comum. Ela esconde padrões numéricos que matemáticos e cientistas estudam há séculos. Esses padrões aparecem em várias áreas, como na natureza, arquitetura e arte.
A origem da série de Fibonacci.
O matemático italiano Leonardo Pisano Bigollo, conhecido como Fibonacci, descobriu a sequência no século 13. Ele a usou em "Liber Abaci" para resolver problemas de criação de coelhos. Desde então, a progressão geométrica encanta muitos, mostrando a beleza dos números de Fibonacci.
"A Sequência de Fibonacci é considerada uma das progressões matemáticas mais fascinantes que se manifestam na natureza."
A Sequência de Fibonacci na Natureza
A sequência de Fibonacci não é só uma curiosidade matemática. Ela aparece em muitos fenômenos naturais. Por exemplo, em espirais logarítmicas em conchas marinhas, em arranjos de sementes em girassóis, e em estruturas de folhas de plantas.
Esses padrões naturais mostram a beleza da matemática escondida ao nosso redor. Eles revelam a perfeição da Sequência de Fibonacci na natureza.
Um exemplo incrível é a espiral logarítmica em conchas marinhas, como as do nautiloide. Ela está relacionada à proporção áurea, que é fundamental para a Sequência de Fibonacci. Além disso, os arranjos de sementes em girassóis também seguem esses padrões numéricos.
As estruturas das plantas, como a disposição de folhas em caules, também seguem essa incrível sequência de números. A Sequência de Fibonacci é amplamente encontrada na natureza, demonstrando sua presença em diversos aspectos do mundo natural.
Exemplos Fascinantes da Sequência de Fibonacci
A sequência de Fibonacci é incrível na natureza. Ela aparece nas conchas marinhas e nos girassóis.
Espirais Logarítmicas nas Conchas Marinhas.
As conchas de moluscos, como o caramujo, têm uma estrutura em espiral. Ela segue a espiral logarítmica da sequência de Fibonacci. Essa forma ajuda o animal a crescer de forma eficiente.
A estrutura dessas conchas é incrível. Ela mostra como a sequência de Fibonacci aparece na natureza. Ela cria padrões belos e úteis.
Padrões de Sementes em Girassóis.
Os girassóis também mostram a sequência de Fibonacci. As sementes estão dispostas em um padrão espiral. Esse padrão segue a razão áurea da sequência.
Esse arranjo ajuda a acomodar mais sementes no girassol. É mais um exemplo da sequência de Fibonacci na natureza.
Aplicações Práticas da Sequência de Fibonacci
A sequência de Fibonacci não é só para a natureza. Ela é aplicada em diversas disciplinas, incluindo arquitetura e design. Arquitetos e designers usam essa sequência para criar coisas bonitas e harmoniosas.
Fibonacci na arquitetura e design.
Na arquitetura, a sequência de Fibonacci contribui para estabelecer proporções e estruturar fachadas. Isso cria coisas que são agradáveis para ver e harmoniosas.
Arquitetos famosos, como Frank Lloyd Wright e Le Corbusier, usaram a sequência de Fibonacci em seus projetos. Eles criaram coisas que lembram a beleza da natureza. No design, ela ajuda a organizar elementos em embalagens e logotipos.
| Área | Aplicação da Sequência de Fibonacci |
|---|---|
| Arquitetura | Proporções em fachadas, estruturas, disposição de elementos |
| Design | Layouts, composição de embalagens, logotipos, proporção de móveis |
Usando a sequência de Fibonacci, profissionais de arquitetura e design criam coisas bonitas. Eles fazem obras que são atraentes e harmoniosas.
Sequência de Fibonacci e a Razão Áurea
A sequência de Fibonacci possui uma ligação significativa com a razão áurea. Ambas revelam a harmonia e padrões ocultos na natureza e na arte. À medida que a sequência avança, a proporção entre os números converge para a razão áurea..
Essa proporção é considerada agradável aos olhos. Ela aparece em fenômenos naturais, como flores e conchas marinhas. Também está na arte. Essa relação revela como a matemática e as proporções se manifestam em contextos surpreendentes.
"A relação entre a matemática e as belezas da natureza é iluminada pela razão áurea."
Explorando essa relação, entendemos melhor a natureza. E podemos usar esses princípios em design, arquitetura e estética.
| Sequência de Fibonacci | Razão Áurea |
|---|---|
| Uma série de números em que cada número é a soma dos dois anteriores | Uma proporção matemática encontrada na natureza e considerada esteticamente agradável |
| Os primeiros números da sequência são: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... | A razão entre números consecutivos da sequência de Fibonacci se aproxima cada vez mais da razão áurea, que é aproximadamente 1,618 |
Entender a relação entre a sequência de Fibonacci e a razão áurea nos ajuda a ver a beleza e a ordem na natureza. E podemos usá-las em nossas criações.
Recursão Matemática por Trás da Sequência.
A sequência de Fibonacci é baseada em um conceito chamado recursão. Cada número é obtido pela soma dos dois anteriores, formando assim uma sequência singular e fascinante.
Essa estrutura recursiva aparece em muitos fenômenos naturais. Ela é uma ferramenta poderosa para entender padrões complexos. Ao explorar a recursão matemática da sequência de Fibonacci, aprendemos mais sobre a natureza.
A sequência começa com 0 e 1. Depois, cada número é a soma dos dois anteriores. Por exemplo: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 e assim por diante.
Esse padrão de progressão geométrica é incrível. Ele aparece em muitas coisas da natureza. Como as espirais em conchas marinhas e os arranjos de sementes em girassóis.
| Termo | Valor |
|---|---|
| F0 | 0 |
| F1 | 1 |
| F2 | 1 |
| F3 | 2 |
| F4 | 3 |
| F5 | 5 |
| F6 | 8 |
A matemática por trás da sequência de Fibonacci é incrível. Ela mostra a beleza e elegância da natureza.

A Beleza dos Números de Fibonacci.
Os números da Sequência de Fibonacci são vistos como muito agradáveis. Eles estão ligados a padrões de simetria e proporções na natureza. Folhas, flores e estruturas animais mostram essa conexão. Isso inspira artistas e designers a explorar a elegância dos "números mágicos".
Simetria e Padrões na Natureza.
Na natureza, os números de Fibonacci aparecem em muitas formas. Conchas, sementes de girassóis e o crescimento de plantas são alguns exemplos. Essa conexão entre matemática e natureza é fascinante.
• As espirais em conchas marinhas seguem a Sequência de Fibonacci, mostrando uma simetria impressionante.
• O arranjo de sementes em girassóis também segue essa sequência, criando uma estrutura atraente.
• O crescimento de folhas e galhos em plantas segue a Razão Áurea, resultando em padrões elegantes.
Essa relação entre matemática e natureza é uma poderosa fonte de inspiração. Mostra a beleza e elegância dos números de Fibonacci.
" Na natureza, existe um vasto manancial de soluções engenhosas e eficazes. A Sequência de Fibonacci é um dos seus principais instrumentos."
Sequência de Fibonacci nas Artes e Cultura.
A sequência de fibonacci não é só de matemática e natureza. Ela também influenciou muito as artes e a cultura. Artistas, arquitetos e designers de todo o mundo usaram sua beleza e harmonia para criar obras-primas. Essas obras revelam a essência da cultura e da arte.
Na pintura e escultura, até na arquitetura e design, a sequência de fibonacci aparece. Ela mostra sua versatilidade e importância. Essa conexão entre matemática e arte nos faz ver a sequência de fibonacci de outra forma.
Na arquitetura e no design, a sequência de fibonacci é usada para criar coisas impressionantes. É incrível ver como ela pode ser usada de tantas maneiras. Ela une matemática, arte e cultura de forma bela.
Explorando a influência da sequência de fibonacci nas artes e cultura, vemos como matemática e arte se unem. Essa união nos ajuda a entender melhor o mundo. Ela nos motiva a procurar beleza e perfeição em tudo que realizamos.

Curiosidades sobre a Sequência de Fibonacci.
A Sequência de Fibonacci é mais que uma série de números. Foi descoberta pelo matemático italiano Leonardo de Pisa, conhecido como Fibonacci. Ela esconde muitas curiosidades que mostram sua importância e beleza.
Você sabia que os números de Fibonacci aparecem em locais inesperados? Por exemplo, na disposição de folhas em plantas, no ritmo cardíaco de seres vivos e na estrutura de teias de aranhas. Essa sequência também tem propriedades matemáticas incríveis, como a relação com a Razão Áurea e a conexão com a espiral de Fibonacci.
• Os números de Fibonacci podem ser observados na disposição de folhas em caules de plantas, como no girassol e na inflorescência da alcachofra.
• A Sequência de Fibonacci está presente no padrão de crescimento de conchas marinhas, como a concha de nautilus.
• Essa série numérica também aparece no ritmo cardíaco de diversos seres vivos, incluindo o ser humano.
• As teias de aranhas exibem uma organização geométrica baseada na espiral de Fibonacci.
Explorar essas curiosidades sobre a Sequência de Fibonacci nos ajuda a entender melhor sua beleza e complexidade. Ela está profundamente ligada à natureza e ao universo que nos cerca.
Entendendo a Sequência de Fibonacci na Programação.
A sequência de Fibonacci é amplamente reconhecida por sua importância na matemática e na programação, aplicada em diversos algoritmos e problemas computacionais. Ela é definida pela seguinte relação recursiva:
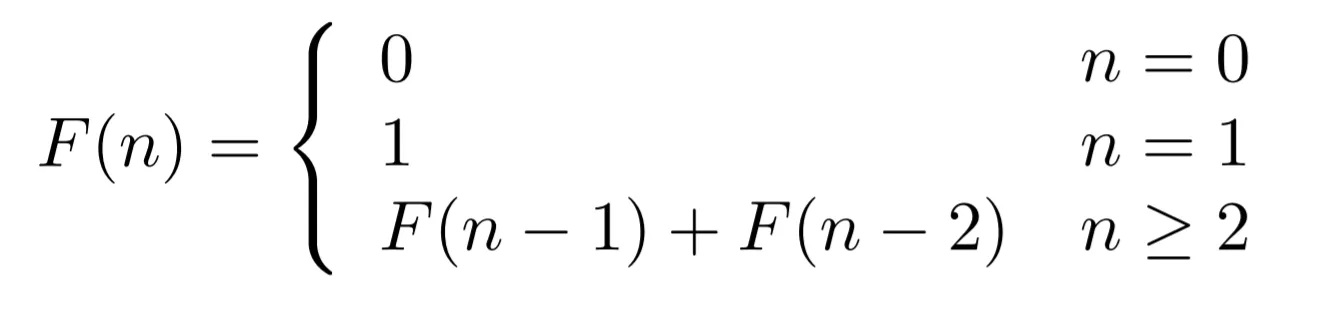
Implementação em Python.
Vamos explorar como implementar a sequência de Fibonacci em Python, utilizando o método iterativo fornecido:
def formatar_mensagem(mensagem, cor_codigo):
return f"\033[{cor_codigo}m{mensagem}\033[m"
def solicitar_numero_fibonacci():
while True:
try:
numero = int(input(formatar_mensagem('Por favor, digite até onde deve ir a sequência de Fibonacci: ', '1;35')))
if numero < 0:
print(formatar_mensagem('Por favor, digite um número inteiro positivo.', '1;31'))
else:
return numero
except ValueError:
print(formatar_mensagem('Entrada inválida. Por favor, digite um número inteiro.', '1;31'))
# Exemplo de uso
numero = solicitar_numero_fibonacci()
# Inicializando os dois primeiros números da sequência
a, b = 0, 1
# Imprimindo os primeiros 'numero' números da sequência
print(formatar_mensagem('A sequência de Fibonacci.', '1;35'))
for i in range(numero):
print(formatar_mensagem(f"{a}", '1;33'), end=' ')
a, b = b, a + b
Neste código:
- `numero` representa até onde queremos gerar a sequência de Fibonacci.
- Usamos duas variáveis `a` e `b` para armazenar os dois últimos números da sequência.
- O loop `for` itera `numero` vezes, imprimindo cada número da sequência.
Fórmula Alternativa.
O código inicialmente fornecido utiliza uma fórmula alternativa para calcular diretamente o n-ésimo termo da sequência de Fibonacci usando a fórmula de Binet:
def formatar_mensagem(mensagem, cor_codigo):
return f"\033[{cor_codigo}m{mensagem}\033[m"
def solicitar_numero_fibonacci():
while True:
try:
numero = int(input(formatar_mensagem('Por favor, digite até onde deve ir a sequência de Fibonacci: ', '1;35')))
if numero < 0:
print(formatar_mensagem('Por favor, digite um número inteiro positivo.', '1;31'))
else:
return numero
except ValueError:
print(formatar_mensagem('Entrada inválida. Por favor, digite um número inteiro.', '1;31'))
# Exemplo de uso
numero = solicitar_numero_fibonacci()
n = 0
while n < numero:
resultado_sequencia_fibonacci = (pow((1 + pow(5, 1 / 2)) / 2, n) - pow((1 - pow(5, 1 / 2)) / 2, n)) / (
pow(5, 1 / 2))
n = n + 1
print(formatar_mensagem(f'\033[1;31mO valor da sequência de Fibonacci na posição {numero} é '
f'{resultado_sequencia_fibonacci:.0f}\033[m', '1;35'))
Neste código:
- `numero` é o número de termos que queremos calcular.
- `n` é usado para iterar através dos termos da sequência.
- A fórmula de Binet é utilizada para calcular diretamente o n-ésimo termo da sequência de Fibonacci.
Conclusão.
Exploramos a Sequência de Fibonacci, uma série numérica que mostra padrões incríveis na natureza. Ela aparece em conchas marinhas e sementes de girassol. Também vimos como ela influencia arte e arquitetura.
A Sequência de Fibonacci mostra a beleza da matemática e da natureza. Ela nos faz ver a elegância e perfeição dos padrões naturais. Esses números mágicos revelam a complexidade do nosso mundo.
Esta jornada me fez ver a natureza de uma nova maneira. Estou mais atento aos padrões fascinantes que a Sequência de Fibonacci nos mostra. É uma das maiores expressões da beleza matemática que conhecemos.
Na programação, a sequência de Fibonacci não apenas ilustra conceitos matemáticos fundamentais, mas também demonstra a versatilidade de abordagens computacionais. Desde uma implementação simples, iterativa até fórmulas mais complexas como a de Binet, entender e aplicar a sequência de Fibonacci é essencial para qualquer programador em busca de soluções eficientes e elegantes. Através da matemática, podemos não só resolver problemas práticos, mas também descobrir padrões que ecoam na beleza e na complexidade encontradas na natureza.
Espero que este artigo tenha ajudado a entender melhor como implementar a sequência de Fibonacci em Python e como aplicá-la em diferentes contextos de programação.
FAQ
A Sequência de Fibonacci consiste em uma série numérica em que cada número é a soma dos dois que o precedem.
Ela começa com 0 e 1, e continua com 1, 2, 3, 5, 8, 13, 21, e assim por diante.
Essa sequência foi descrita pelo matemático italiano Leonardo Pisano Bigollo, mais conhecido como Fibonacci, no século XIII.
A Sequência de Fibonacci se manifesta em diversos fenômenos da natureza. Ela se vê em espirais logarítmicas de conchas marinhas e em arranjos de sementes em girassóis.
Além disso, ela aparece em estruturas de folhas de plantas. Esses padrões mostram a beleza e perfeição da matemática na natureza.
A Sequência de Fibonacci se revela de forma fascinante na natureza, como nas espirais logarítmicas das conchas marinhas e nos padrões das sementes de girassóis.
Esses padrões seguem a lógica da sequência, criando formas elegantes e eficientes. Eles mostram como a matemática se expressa de maneira bela na natureza.
A Sequência de Fibonacci é usada na arquitetura e no design. Arquitetos e designers se inspiram nela para criar estruturas e layouts harmoniosos.
Desde a disposição de elementos em fachadas de prédios até a proporção de móveis e embalagens, a Sequência de Fibonacci ajuda a alcançar equilíbrio e beleza.
A Sequência de Fibonacci tem uma conexão com a Razão Áurea. Essa proporção é considerada esteticamente agradável e aparece em muitos fenômenos naturais e artísticos.
À medida que a sequência avança, a razão entre números consecutivos se aproxima da Razão Áurea. Essa conexão mostra a harmonia e padrões escondidos na natureza e na arte.
A Sequência de Fibonacci é construída com base em um princípio matemático chamado recursão. Cada número é calculado pela soma dos dois números que o precedem.
Essa estrutura recursiva está presente em diversos fenômenos naturais. Investigar a matemática da Sequência de Fibonacci nos permite entender melhor a natureza e suas estruturas subjacentes.
A Sequência de Fibonacci tem muitas curiosidades interessantes. Por exemplo, os números de Fibonacci aparecem em inesperadas situações, como na disposição de folhas em plantas e no ritmo cardíaco de seres vivos.
Além disso, essa série numérica possui propriedades matemáticas fascinantes. Ela está relacionada à Razão Áurea e à espiral de Fibonacci, uma forma geométrica presente em muitos sistemas naturais.
Autor