Sumário
Diagonal Principal - Atenção: Com o algorítimo utilizado podemos efetuar a soma de qualquer matriz quadrada não sendo somente uma matriz 3x3.
Antes de começarmos temos que fala sobre a diferença na indexação.
A diferença na indexação entre a matemática (onde muitas vezes começamos a contar a partir de 1) e a programação (onde começamos a contar a partir de 0) é uma fonte comum de confusão para iniciantes na programação. Vamos explorar essa diferença e explicar como ela afeta o acesso aos elementos em uma matriz.
Matemática: Indexação começando por 1
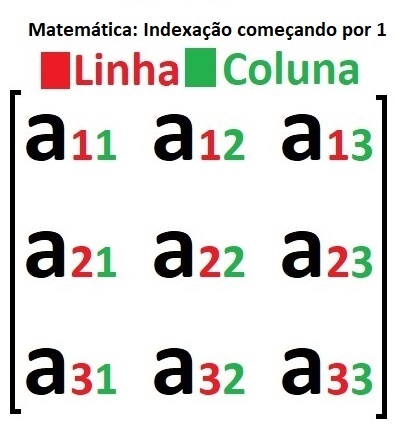
Na matemática e em muitas áreas de estudo acadêmico, como em álgebra linear e teoria dos grafos, é comum começar a contar a partir do número 1. Por exemplo, ao descrever uma matriz ou um sistema de coordenadas:
- Matriz: Os elementos são identificados com dois índices, onde o primeiro índice representa a linha e o segundo índice representa a coluna.
Em uma matriz 3x3, por exemplo, o elemento na primeira linha e primeira coluna é referido como (1,1), na segunda linha e segunda coluna é (2,2), e assim por diante.
Programação: Indexação começando por 0
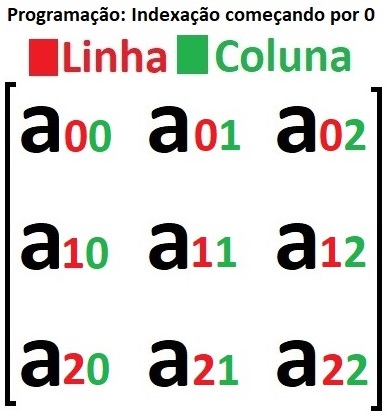
Por outro lado, na programação e na maioria das linguagens de programação, a indexação geralmente começa em 0. Isso significa que o primeiro elemento em uma lista, array ou matriz é acessado pelo índice 0, o segundo pelo índice 1, e assim por diante. Isso é especialmente comum em linguagens como Python, C, Java, JavaScript, entre outras.
Depois desse esclarecimento, vamos continuar!!
Introdução
Vou mostrar como calcular a soma da diagonal principal de uma matriz 3×3 em Python que é uma linguagem muito eficaz para lidar com matrizes. Saber fazer isso é essencial em muitos campos da computação.
Matrizes são muito importantes na programação. Entender como trabalhar com elas é fundamental. Vamos abordar desde os princípios básicos até as técnicas mais sofisticadas. Focaremos na soma da diagonal principal de uma matriz 3x3 em Python.
Manipular matrizes é fundamental na programação, especialmente em áreas como ciência de dados e engenharia. Neste tutorial, abordaremos um exemplo prático de como manipular uma matriz 3x3 em Python, focando na soma dos elementos da diagonal principal. Essa habilidade é essencial para várias aplicações, incluindo cálculos de estatísticas, transformações matriciais e otimização de algoritmos numéricos. A compreensão profunda das operações matriciais permite desenvolver soluções eficientes e robustas para uma ampla gama de problemas computacionais e analíticos.

Este guia abrange desde a representação de matrizes em Python até métodos avançados. Você vai aprender a fazer um algoritmo para calcular a soma da diagonal principal. Também vai ver como usar esse conhecimento em prática.
Principais Pontos
• Conceitos fundamentais de matrizes em Python
• Execução detalhada do cálculo da soma diagonal
• Técnicas avançadas para manipulação de matrizes
• Aplicações de Álgebra Linear no Processamento de Imagens
• Otimização de código para matrizes maiores
• Dicas para evitar erros comuns na programação com matrizes
Introdução às Matrizes em Python.
As matrizes são estruturas de dados essenciais na programação, consistindo em coleções de elementos dispostos em linhas e colunas. São essenciais para quem começa com Python.
O que são matrizes?
Matrizes são coleções de números organizados em linhas e colunas, e em Python, representamos matrizes usando listas de listas. As matrizes são amplamente usadas em cálculos científicos, análise de dados e inteligência artificial, tornando-se um conceito essencial para programadores iniciantes e avançados.
Como representar matrizes em Python.
Para representar matrizes em Python, usamos listas de listas. Aqui está um exemplo de uma matriz 3x3:
| Linha/Coluna | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | 2 | 3 |
| 1 | 4 | 5 | 6 |
| 2 | 7 | 8 | 9 |
Dica: Se a matriz não for quadrada (ou seja, se tiver um número diferente de linhas e colunas), então não haverá uma diagonal principal completa para calcular a soma.
Outra imagem de exemplo.

Em Python, essa matriz seria representada assim:
matriz = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Importância das matrizes na programação.
As matrizes são essenciais em diversos algoritmos e aplicações. Elas são usadas em:
• Processamento de imagens
• Cálculos científicos
• Análise de dados
• Inteligência artificial
Conhecer bem as matrizes é crucial para quem aprende Python. Elas auxiliam na resolução de problemas complexos de maneira eficiente, o que torna o aprendizado da programação mais acessível para iniciantes.
Entendendo a Diagonal Principal de uma Matriz.
As matrizes são muito importantes na programação. As diagonais principais têm um papel chave. Elas são essenciais para quem trabalha com álgebra linear e programação.
A diagonal principal é composta por elementos cujos índices de linha e coluna são iguais. Em uma matriz 3x3, por exemplo, inclui os elementos nas posições (0,0), (1,1) e (2,2).
Os elementos em itálico (5, 9 e 6) formam a diagonal principal. Na programação, trabalhar com essas diagonais é comum. Isso inclui desde cálculos matemáticos até processamento de imagens.
"A diagonal principal é uma ferramenta poderosa na álgebra linear, servindo como base para conceitos avançados como determinantes e autovalores."
Entender as diagonais principais é crucial para criar algoritmos eficientes. Isso é válido para Python e outras linguagens. Esse conhecimento ajuda a encontrar soluções criativas em vários campos da computação.
Calculando a Soma dos Elementos da Diagonal Principal de uma Matriz 3×3 Python.
Vamos aprender a somar os elementos da diagonal principal de uma matriz 3x3 em Python. Este método é essencial na matemática computacional. Ele tem muitas aplicações práticas.
Passo a passo do algoritmo.
O algoritmo para somar a diagonal principal é fácil:
1. Criar a matriz 3x3
2. Definir uma variável para a soma
3. Andar pela diagonal principal
4. Adicionar os elementos encontrados
5. Mostrar o resultado
Implementação do código em Python.
Veja um exemplo de código Python para fazer isso:
def soma_diagonal(matriz):
soma = 0
for i in range(3):
soma += matriz[i][i]
return soma
matriz = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
resultado = soma_diagonal(matriz)
print(f"A soma da diagonal principal é: {resultado}")

Explicação detalhada do funcionamento.
Este código faz operações matemáticas simples, mas eficazes. A função soma_diagonal vai pela diagonal principal da matriz. Essa é a linha em que o índice da linha coincide com o índice da coluna. Em cada passo, adicionamos o elemento atual à variável soma. No fim, devolvemos o total.
Na matemática computacional, esse processo é otimizado para matrizes de qualquer tamanho. Não só para 3x3. Essa técnica é muito usada em álgebra linear e em processamento de dados multidimensionais.
Vejamos agora um segundo código, mas avançado, que não faz uso de nenhuma biblioteca:
def obter_numero(mensagem):
while True:
try:
return int(input(mensagem))
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
def verifica_matriz_quadrada(num_linhas, num_colunas):
if num_linhas != num_colunas:
print(
'\033[1;31mErro: Esta implementação suporta apenas matrizes quadradas (mesmo número de linhas e colunas). '
'Reiniciando o programa...\033[m')
main() # Reinicia o programa
def criar_matriz(num_linha, num_coluna):
matriz = []
for linha_numero in range(num_linha):
linha = []
for coluna_numero in range(num_coluna):
while True:
try:
valor = int(
input(f'\033[1;35mPor Favor, digite o {coluna_numero + 1}º elemento da {linha_numero + 1}º '
f'linha: \033[m'))
linha.append(valor)
break
except ValueError:
print('\033[1;31mValor INVÁLIDO! Digite apenas números!\033[m')
matriz.append(linha)
return matriz
def calcular_soma_diagonal_principal(matriz):
diagonal_principal = []
soma = 0
for i in range(len(matriz)):
diagonal_principal.append(matriz[i][i])
soma += matriz[i][i]
print(f'\033[1;31mOs elementos da diagonal principal é {diagonal_principal}.\033[m')
return soma
def mostrar_matriz(matriz):
print('\n\033[1;36mMatriz gerada:\033[m')
for linha in matriz:
print(f'\033[1;36m{linha}\033[m')
def main():
print('\033[1;41m*** Inicializando o programa ***\033[m\n')
numero_linhas = obter_numero('\033[1;34mDigite o número de linhas da matriz: \033[m')
numero_colunas = obter_numero('\033[1;34mDigite o número de colunas da matriz: \033[m')
verifica_matriz_quadrada(numero_linhas, numero_colunas)
matriz = criar_matriz(numero_linhas, numero_colunas)
print('\n\033[1;34mMatriz inserida:\033[m')
mostrar_matriz(matriz)
soma_diagonal = calcular_soma_diagonal_principal(matriz)
print(f'\n\033[1;34mA soma dos elementos da diagonal principal da matriz é: {soma_diagonal}\n\033[m')
if __name__ == "__main__":
while True:
main()
continuar = input('\033[1;35mDeseja calcular para outra matriz? (s/n): \033[m').lower()
if continuar != 's':
print('\033[1;33mFinalizando o programa!!!!\033[m')
break
Explicação do Código
1. Definição da Matriz: A função `criar_matriz` permite ao usuário inserir os elementos de uma matriz 3x3.
2. Cálculo da Soma da Diagonal Principal: A função `calcula_soma_diagonal_principal` percorre a diagonal principal da matriz e calcula a soma dos elementos.
3. Exibição da Matriz: A função `mostrar_matriz` formata e exibe a matriz na tela.
Técnicas Avançadas para Manipulação de Matrizes em Python.
Na programação Python, saber manipular matrizes é crucial. Vou mostrar algumas técnicas avançadas para trabalhar com essas estruturas.

A biblioteca NumPy muda o jogo ao lidar com matrizes. Ela torna operações complexas simples e rápidas. Vejamos um exemplo:
import numpy as np
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
soma_diagonal = np.trace(matriz)
print(f"Soma da diagonal principal: {soma_diagonal}")
Este exemplo mostra como o NumPy facilita o cálculo da soma da diagonal principal. A função trace() faz o trabalho pesado por nós, melhorando a performance.
Outra técnica importante é a multiplicação de matrizes com NumPy:
matriz_a = np.array([[1, 2], [3, 4]])
matriz_b = np.array([[5, 6], [7, 8]])
resultado = np.dot(matriz_a, matriz_b)
print("Resultado da multiplicação:")
print(resultado)
A função dot() faz a multiplicação matricial de forma eficiente. Isso é essencial em cálculos complexos de álgebra linear.
Para quem quer melhorar na programação Python, dominar essas técnicas é muito importante.
| Técnica | Benefício | Aplicação |
|---|---|---|
| NumPy Arrays | Operações vetorizadas rápidas | Cálculos científicos |
| Slicing avançado | Acesso eficiente a submatrizes | Processamento de imagens |
| Broadcasting | Operações entre arrays de diferentes formas | Análise de dados |
Aplicações Práticas da Soma da Diagonal Principal.
A soma da diagonal principal de uma matriz é muito usada em várias áreas. Ela aparece na álgebra linear, no processamento de imagens e no aprendizado de máquina. Vamos ver como isso funciona em cada um desses campos.

Uso em álgebra linear.
Na álgebra linear, referimos a isso como traço da matriz. O traço é muito importante para calcular determinantes e autovalores. Ele também auxilia na resolução de sistemas de equações lineares.
Em algoritmos de otimização, o traço simplifica as operações matriciais. Isso torna o trabalho mais fácil.
Aplicações em processamento de imagens.
Para processar imagens, a diagonal principal é essencial. Ela é usada em técnicas de compressão e filtragem. Por exemplo, ajuda a detectar bordas em imagens.
Utilização em aprendizado de máquina.
No aprendizado de máquina, a diagonal principal é usada para reduzir dimensionalidade. Isso é feito através da Análise de Componentes Principais (PCA). Ela também é importante em algoritmos de clustering para analisar a dispersão dos dados.
| Área | Aplicação | Benefício |
|---|---|---|
| Álgebra Linear | Cálculo de determinantes | Simplifica operações matriciais |
| Processamento de Imagens | Detecção de bordas | Melhora a identificação de padrões |
| Aprendizado de Máquina | Redução de dimensionalidade | Otimiza a análise de dados complexos |
Essas aplicações mostram o impacto da matemática computacional em várias áreas. Elas nos ajudam a criar algoritmos mais eficientes. Dessa forma, podemos abordar problemas complexos de maneira criativa.
Otimizando o Código para Matrizes Maiores.
Trabalhar com matrizes grandes em Python exige otimização. Vou mostrar técnicas para aumentar a eficiência na soma da diagonal principal.
Uma boa estratégia é usar compreensão de lista. Essa técnica da lógica de programação cria listas rapidamente:
soma = sum(matriz[i][i] for i in range(len(matriz)))
Outra maneira é usar a biblioteca NumPy. Ela é especializada em cálculos numéricos:
import numpy as np
matriz = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
soma = np.trace(matriz)
O NumPy tem funções otimizadas, como 'trace()'. Elas são perfeitas para grandes matrizes em Python.
Para matrizes muito grandes, pense em processamento paralelo. A biblioteca 'multiprocessing' divide o trabalho entre CPUs. Isso diminui muito o tempo de execução.
A escolha da técnica varia com o tamanho da matriz e os recursos. Teste várias abordagens para achar a melhor para seu caso.
Erros Comuns e Como Evitá-los.
Trabalhar com estruturas de dados em Python pode ser desafiador para iniciantes. Vamos ver os erros mais comuns e como resolver eles.
Problemas de indexação.
Um erro comum é a indexação incorreta. Lembre-se de que, em Python, a contagem de índices começa em zero. Verifique se está acessando o índice certo da sua matriz.
Confusão entre listas e matrizes.
Muitos confundem listas e matrizes em Python. Listas são nativas, mas matrizes usam NumPy. Para usar matrizes, importe o NumPy.
Dicas para depuração eficiente.
Depuração é crucial com dados complexos. Use print para ver o conteúdo das matrizes. O debugger do Python também ajuda a encontrar erros.
| Erro | Causa | Solução |
|---|---|---|
| IndexError | Acessar índice inexistente | Verificar limites da matriz |
| TypeError | Operações incompatíveis | Confirmar tipos de dados |
| ValueError | Operações inválidas | Validar entrada de dados |
Evitar esses erros e usar técnicas de depuração melhora a programação com matrizes em Python.
Comparação com Outras Linguagens de Programação.
Na programação python, somar a diagonal principal de uma matriz 3x3 é simples. Vamos ver como o Python se compara com outras linguagens populares. Isso mostra as vantagens do Python nesse aspecto.
Em C++, fazer isso requer mais linhas de código e uma sintaxe mais complexa. Em Java, a abordagem é semelhante, mas com diferenças na declaração de variáveis e loops. O Python se destaca pela simplicidade e clareza dos seus algoritmos.
| Linguagem | Linhas de Código | Complexidade |
|---|---|---|
| Python | 3-5 | Baixa |
| C++ | 10-15 | Média |
| Java | 8-12 | Média |
A sintaxe concisa do Python permite resolver este problema em poucas linhas. Isso faz do Python a escolha perfeita para prototipagem rápida e análise de dados. Além disso, a rica biblioteca padrão do Python oferece ferramentas poderosas para manipulação de matrizes, como o NumPy.
Em resumo, embora outras linguagens possam ser mais rápidas em termos de desempenho, o Python oferece um equilíbrio único. Ele é fácil de usar e tem poder computacional para tarefas de algoritmos matriciais.
Recursos Adicionais para Aprofundamento.
Quer aprender mais sobre python para iniciantes e matemática computacional? Tenho alguns recursos incríveis para você. Eles vão ajudar a aprimorar seus conhecimentos em Python e trabalhar com matrizes.
Livros recomendados.
Existem livros ótimos para quem começa com python e matemática computacional. "Python para Análise de Dados" de Wes McKinney e "Matemática Computacional com Python" de Claus Führer são excelentes escolhas.
Cursos online.
Plataformas de ensino online têm cursos incríveis sobre Python e matemática computacional. No Coursera, o curso "Python para Todos" da Universidade de Michigan é perfeito para iniciantes. Já no edX, o "Introdução à Matemática Computacional" do MIT é uma ótima opção.
Comunidades e fóruns de discussão.
Participar de comunidades online é essencial para crescer. O Stack Overflow é ótimo para resolver dúvidas de programação. No Reddit, as comunidades r/learnpython e r/mathprogramming são ótimas para se conectar com outros entusiastas.
| Recurso | Tipo | Foco |
|---|---|---|
| Python para Análise de Dados | Livro | Python e análise de dados |
| Python para Todos | Curso online | Fundamentos de Python |
| Stack Overflow | Fórum | Dúvidas de programação |
Praticar sempre é crucial. Explore esses recursos, faça exercícios e não tenha medo de pedir ajuda. Com esforço, você vai dominar python para iniciantes e matemática computacional rapidamente.
Conclusão
Neste artigo, exploramos o fascinante mundo das matrizes em Python. Aprendemos a calcular a soma da diagonal principal de uma matriz 3x3. Essa habilidade é muito útil para programadores e entusiastas de matemática.
Calcular a soma da diagonal principal de uma matriz 3x3 em Python é uma tarefa fácil. Essa técnica é útil em várias áreas. Ela é usada em álgebra linear, processamento de imagens e aprendizado de máquina.
Ter essa habilidade é só o começo. Há muito mais a explorar nas matrizes. Encorajo você a continuar aprendendo e melhorando suas habilidades nesse campo fascinante.
Se este tutorial foi útil para você, não hesite em compartilhá-lo com seus colegas. Continue explorando nosso blog para mais tutoriais práticos de Python e aprofunde seus conhecimentos em programação matricial e além.
FAQ
Matrizes são estruturas de dados compostas por valores organizados em linhas e colunas. Elas são representadas por listas aninhadas em Python. Isso permite fazer operações matemáticas e manipular dados de forma eficiente.
A diagonal principal começa no canto superior esquerdo e vai até o canto inferior direito. Em uma matriz 3×3, esses elementos estão nas posições (0,0), (1,1) e (2,2).
Calcular a soma da diagonal principal é essencial em álgebra linear. Tem uso em processamento de imagens, aprendizado de máquina e análise de dados.
Sim, é possível otimizar o código para matrizes grandes. Usar bibliotecas como NumPy pode ajudar muito.
Erros comuns incluem problemas de indexação e confusão entre listas e matrizes. Também é comum ter dificuldades na depuração. É crucial seguir boas práticas para evitar esses erros.
Há muitos recursos para aprender mais, como livros e cursos online. Comunidades e fóruns também são ótimos para discutir sobre Python e estruturas de dados. Sugiro que você explore essas opções para aprofundar seus conhecimentos.
Autor